what's the siney graph in your header?

I encourage anyone reading this to read as much or as little as they want. I hope that anyone can understand the detailed explanation, and that most math undergrads can understand most of the observations I make. The generalisations might not be so accessible all the time.

To put it tersely, its the projection of the barycentric subdivision of a tetrahedron onto the 2-sphere, visualised on a rectangle via the mercator projection.

This is closely related to Coxeter groups, the classification of polytopes, the classification of straight line Coxeter groups, the classification of regular tilings of surfaces of constant curvature, and Schl\"afli symbols.

A more detailed explanation:

Imagine taking a tetrahedron, putting a dot on the middle of each vertex, edge, and face, and connecting them all up with straight lines along its surface. This is the so called "barycentric subdivision". Then consider the origin to be in the middle of the tetrahedron, and then project the tetrahedron (and the lines we drew on it) onto a sphere. We use the mercator projection to view it like a map, but we still think of it as lying on the sphere (see below mp4 of said sphere with the barycentric subdivision drawn on it). Each face of the tetrahedron could be imagined to be coloured a certain colour, so v_2 in the diagram on my header is the vertex at the centre of the yellow face, v_1 is the vertex in the centre of one of the yellow faces edges, and similarly for v_0. These appear to be connected by curved lines, but these are straight lines on the surface of the sphere.

Assume the tetrahedron and sphere are embedded in R^3 and share a common centre at the origin.

Some interesting observations:

each of these lines we drew now gets turned into a great circle, which corresponds to a plane going through the origin

reflections in these great circles preserves the lines we drew, and correspond to automorphisms of the tetrahedron

each triangle in the subdivision has angles pi/3 radians, pi/3 radians, and pi/2 radians.

the symmetry group of the tetrahedron is S_4, where the adjacent transpositions correspond to permutations of the faces (or if you like, vertices)

the symmetric group S_4 has a presentation , where the s_i are adjacent transpositions of 4-tuples

The exponents of the (s_is_j) terms above exactly match the denominators of the angles of the triangle mentioned above

we can pick one triangle on the sphere and consider the reflections in (the faces corresponding to) its edges, denoted s_0, s_1, and s_2. These reflections permute the coloured faces of the tetrahedron, or if you like, its vertices.

we can repeatedly apply these reflections to flip across an edge or vertex of the yellow face, rotate about the centre of the yellow face (e.g. s_0 s_1), and transpose the yellow face with any other face

In this manner we can represent every symmetry of the barycentric subdivision, and by extension, the tetrahedron, in terms of these three reflections. If you don't see this, consider the effect of conjugation.

The sphere is a surface of constant curvature

This tiling generated by the tetrahedron is a regular tiling of the sphere

In short, the tetrahedron has a symmetry group S_4 (often called A_4 in analogy with the Dynkin Diagram) that has a presentation in terms of three reflections, which act transitively on this barycentric subdivision. The angles of the barycentric subdivision correspond to the relations of the presentation. One can generalise this observation and use it to classify polyhedra.

Some theoretical results.

A Coxeter group is a group W accompanied by a set of generators S = {s_1, s_2, ..., s_n} \subseteq W, such that W = <s_i | (s_is_j)^m(i,j) = 1>, where m(i,j) is an integer at least 1, m(i,i) = 1, and m(i,j) > 1 if i != j. These relations turn out to exactly correspond to the relations necessary to define a finite system of reflections in (n+1)-dimensional space.

By polytope, I mean a bounded convex polytope.

The regular tilings of the sphere correspond to regular polytopes, which correspond to the finite irreducible Coxeter groups whose Dynkin diagrams have straight lines

We can define a polytope to be regular if the automorphism group of the polytope acts transitively on the regions of the barycentric subdivision (or equivalently, its "flags"), which corresponds to chains of i-faces of the polytope ordered by inclusion

To go from a polytope to its Coxeter group, you take its automorphism group to get the group structure, and do a similar thing to above to find the generators, you arrange some hyperplanes so that their reflections satisfy the relations of the Coxeter group, generate a system of hyperplanes closed under reflection, and intersect this with an (n-1)-sphere to get the barycentric subdivision, from which you can recover a polytope and its dual polytope, which have isomorphic Coxeter groups

The regular tilings of the plane correspond to the affine irreducible Coxeter groups with straight line Dynkin diagrams.

One can study the regular tilings of hyperbolic space and classify those Coxeter groups too.

The E_8 lattice, which gives solution to 8-dimensional sphere packing has a a load of other interesting properties, corresponds to the Coxeter group E_8, via a certain semiregular polytope which is the convex hull of some lattice points.

The classification of regular (n-dimensional) polytopes and regular tilings of R^n is via the classification of Coxeter groups (and by extension Dynkin diagrams with certain properties)

There is an elegant classification according to Bourbaki that resembles the typical intuitive classification of regular polyhedra and regular tilings of R^2

Fun extensions

There are a lot of ways to represent a symmetry of a polytope/element of a Coxeter group in terms of the reflections/generators s_i. Is there an easy way to determine whether your representation of the symmetry/group element is the shortest? Yes! In fact, you can construct a DFA on the generators in the finite case.

The Cayley graph of a Coxeter group is Hamiltonian

My pfp shows the duality between an octahedron and a cube. If you draw a vertex at the centre of each face of the cube, and take the convex hull of the vertices, you get an octahedron. Note that vertices of the octahedron correspond to faces of the cube, edges of the octahedron correspond to edges of the cube, and faces of the octahedron correspond to vertices of the cube. Two vertices of the octahedron are incident with each other when the corresponding faces of the cube share an edge, and so on. To put it formally, the poset of i-faces of the octahedron and the poset of i-faces of the cube, both under inclusion, have an anti-isomorphism between them. This causes them to have isomorphic symmetry groups.

The cube has its Coxeter group with relations (s_0s_1)^4 = (s_1s_2)^3 = (s_0s_2)^2 = s_i^2 = 1. Note that here the 4 and 3 are different numbers, and the cube has a dual of an octahedron. In the case of the tetrahedron, the exponents are the same, and the tetrahedron is self dual. In general, finite irreducible Coxeter groups with straight line Dynkin diagrams correspond to self dual polytopes exactly when their Dynkin diagrams are "reversible".

This is heavily related to how the cube and octahedron have reversed Schl\"afli symbols.

What is a Weyl group?

Besides John Baez's  explanation   , I like the one in Coxeter's Regular Polytopes chapter 5. He calls the phenomenon we are describing The Dihedral Kaleidoscope. Take an image in the plane Joan Miró, Women & Birds at Sunrise and reflect it across any of the (half-open) semicircle's worth of options, of lines-thru-the-origin, that you could reflect it across. Call the action of doing this (however you chose the angle) A. Doing A twice is the same as leaving the figure alone, whatever A you chose. But what if you choose two different lines-thru-the-origin to reflect across? Let's call them A≠B. Now these two reflections will interact in some way.† In most cases, A and B will be pointed askew so that they "miss" each other meaning the infinite sequence ABABABAB... never terminates. But there is just one arrangement of two mirrors A & B that will "line up" in the sense that ABAB brings you back to the start. † (Mathematicians dub this interaction a "reflection group" because a   sequence of reflections forms a "generalised multiplication table",   meaning (1) the way I parenthesise sequential reflections doesn't   matter, and (2) reflections are reversible. [any reflection--however you  rotate the "mirror"--is its own opposite, so that's an easy property to  verify.] You can look up the other two "group axioms" on Wikipedia;  making those work is basically a technicality, unlike the deep facts that make special reflection angles special.) If you're doodling the answer or the group-structure to yourself on paper I recommend marking four corners of a square with a,b,c,d. Then use a different colour for each A and B arrow →. (That will make the group structure clear, I think.) Figuring out which mirror angles work is probably easier to think about than to try to draw. But I thought for this answer would look cooler if I pulled the group structure back onto a Miró; hope you like it this way. (And I'll leave it to you to doodle out B then A then B, as well as the other alternatives.) As you add more & more mirrors ABCDE, the angles they should be at to not miss each other follow a predictable pattern. Every mirror you add in this way adds one o to the o―o―o―o―…―o pattern (as drawn in Baez week230). This pattern is called [math]A_n[/math] (n being how many mirrors you put up). (So you can also doodle the reflections of a pentagon, hexagon, .... see What is a group in group-theory? and isomorphismes for more pictures.) What if I were to do something analogous, instead of with a plane figure, with a statue? ↑ The "Lion-Man". Artist unknown, but s/he lived circa 42,000 years ago (=21 Jesuses ago) in the Swabian alps. The figure is famous because it is the most ancient physical proof of human imagination: whoever carved this statue, envisaged something that does not exist in the physical world. (Hint, hint: Dynkin diagrams also do not exist in the physical world.) Well, all of the plane rotations would still group together in the same fashion. So we could still draw Dynkin diagrams like o―o―o―…―o but could also add in more types of reflections, like a "flip-upside-down in the vertical direction" move.    (Let's now rename the old planar reflections A₁, A₂, … to make room for new letters coming from the new dimension. How about calling the upside-down / vertical one U or V?) Besides adding the "upside-down man" reflection, there are other ways to add mirrors that stay in synch / not askew with all of the totality of other mirrors that are already present. There are also some higher-dimensional analogues as well.  (This is one of the harder things to think about in >3D. And also quite hard to think about in 3D, in my opinion. I wrote a blurb about how to visualise higher dimensions and the reflection-group / Buildings view is still on the to-do list. So normally I would say "many dimensions are easier than you think!" but not in this case. For example if you drew a bunch of sticks |||||| -- let's say twenty-seven (http://www.math.harvard.edu/~lurie/papers/thesis.pdf)   --- and marked the + and ‒ ends of each, what reflections would be easy to do by swapping the ± to ∓, and which could you not do that way?) The 120-cell, Schlaefli symbol 5,3,3, physical model by, I believe, P. S. Donchian. That was like a pre-summary of what Coxeter says. Here are a few screenshots from the google preview of Regular Polytopes which explain it better. (You can read the whole chapter on google preview.) Note that this is different to the reflections (which don't go thru the origin) in Thurston's Geometry and Topology of 3-Manifolds: ↑ isomorphismes has more views of this image and a link to GT3M (on msri website). † Maryam Mirzakhani and Alexander Eskin's recent work (   I believe is the relevant IAS link) discusses "billiard-ball dynamics" (they say this is a sort of familiar, but naïve, instantiation of what they do) with a frictionless billiard ball's path. (Strangely after a century of work this is still unsolved.) But again these are not the reflections-thru-the-origin of the so-called "reflection groups" (Coxeter's dihedral kaleidoscope).

the relation of coxeter groups and systems to the symmetries of regular polytopes is really fascinating to me. the fact that you can start with these equivalence classes of strings of letters and end up with descriptions of polytope symmetries with higher dimensions than we'll ever be able to visualise makes sense when you know the context, but it also says something about how important representations and abstractions are to math and how fundamentally related a lot of things are within it. also, coxeter diagrams are pretty neat.

Hypercube, also known as a tesseract, is a fascinating mathematical object that has captured the imagination of mathematicians and physicists alike. It is a higher-dimensional analogue of a cube, possessing more dimensions than the three dimensions we experience in our everyday lives. In this essay, we will explore the properties and characteristics of hypercubes and their applications in mathematics and physics.

A hypercube can be defined as a geometric figure in n dimensions, where n is an integer greater than or equal to 4. In other words, a hypercube is a cube in higher-dimensional space. Just like a cube has six faces, a hypercube has 2^n faces, where n is the number of dimensions. For example, a hypercube in 4 dimensions has 16 faces, while a hypercube in 5 dimensions has 32 faces.

One of the intriguing characteristics of hypercubes is their symmetry. A hypercube possesses a high degree of symmetry because its faces are all congruent and its edges are parallel, making it a regular polytope. This property makes them useful in the study of symmetry groups and the fundamental structure of geometry itself.

Another fascinating property of hypercubes is their ability to tessellate space. A tessellation is a pattern of repeated shapes that covers a plane or a space without any gaps or overlaps. In 3-dimensional space, cubes can tessellate space, but in higher dimensions, only hypercubes can achieve this feat. Hypercubes can tessellate n-dimensional space with parallel and congruent hypercubes, known as a hypercubic honeycomb.

The concept of hypercubes has found applications in various fields, including computer science, physics, and mathematics. In computer science, hypercubes are used in the design of computer networks, particularly in high-performance computing networks. In physics, hypercubes are used to represent the curvature of spacetime in general relativity, a theory that describes the large-scale behavior of the universe. The tesseract has also been used to understand the properties of quantum mechanics, the branch of physics that describes the behavior of matter and energy at the smallest scales.

Furthermore, hypercubes have played a crucial role in the study of dimensions beyond the three we experience in our everyday lives. String theory, a theoretical framework that attempts to reconcile general relativity and quantum mechanics, predicts the existence of extra dimensions beyond the four we know (three dimensions of space and one of time). Hypercubes are used as a tool to visualize these extra dimensions and understand their properties.

In conclusion, hypercubes are fascinating objects that have captured the attention of mathematicians, physicists, and computer scientists. They have important applications in various fields, such as computer science, physics, and mathematics. The regularity and symmetry of hypercubes make them useful in the study of geometry, while their ability to tessellate higher dimensional space is an essential tool in the study of dimensions beyond the three we experience in our everyday lives. As such, hypercubes play a crucial role in advancing our understanding of the fundamental structure of the universe.

Citations:

- Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, pp. 192-207, 1973.

Coxeter non-euclidean geometry pdf worksheets

 COXETER NON-EUCLIDEAN GEOMETRY PDF WORKSHEETS >>Download (Telecharger) vk.cc/c7jKeU

  COXETER NON-EUCLIDEAN GEOMETRY PDF WORKSHEETS >> Lire en ligne bit.do/fSmfG

           of the book is a non-printable .pdf document with hyperlinks. The examples included in the book can be run with just a mouse click and modified and saved by. 8 avr. 2007 — ing mathematical activities in memory of Lang. As H. S. M. Coxeter, whose mension and Non-Euclidean Geometry in Modern. de M Senechal · 1984 · Cité 19fois — Nearly one hundred years ago, a curious geometry book was published in Petersburg,. Russia. Fedorov was not only the first to derive the parallelohedra, requisite of all other mathematical activities if they are forever in circles. Pierpont, James: Non-Euclidean Geometry from Non-Projective Standpoint.Subjects: Geometric Topology (math.GT); Differential Geometry (math.DG); Group Theory (math.GR); Metric Geometry (math.MG); Number Theory (math.NT). de M Hajja · 2008 · Cité 20fois — Coxeter, Introduction to Geometry, John Wiley and Sons, Inc., New York, 1969. [7] A. L. Edmonds, M. Hajja, and H. Martini, Coincidences of 5 sept. 2007 — 9 to 12 and deals with Coxeter's activities after his official a finite set of points in a Euclidean space, not all on a line,. 93 A . T. Fomenko and A. A. Tnzhilin, Element s of the geometry and countries, soon replaced Euclid's theory; in the history of the non-Euclidean.

https://www.tumblr.com/cemovowuri/697951806119182336/iphone-4s-manual-pdf-svenska-lexikon, https://www.tumblr.com/cemovowuri/697951806119182336/iphone-4s-manual-pdf-svenska-lexikon, https://www.tumblr.com/cemovowuri/697951806119182336/iphone-4s-manual-pdf-svenska-lexikon, https://www.tumblr.com/cemovowuri/697951947951669249/cantate-domino-miserachs-pdf, https://www.tumblr.com/cemovowuri/697951806119182336/iphone-4s-manual-pdf-svenska-lexikon.

On Thursday, I went to the ballet lesson and it was nice! We are a small group of eight people and I’ve already liked the teacher before (it must be three years now - tempus fugit!), because she is strict but in a funny and snarky way. Also she was, again, over the moon with my feet, lol (and she isn’t the first). It’s nice she explains everything really detailed now, at the last course I went to it wasn’t that in-depth, because it wasn’t solely for beginners. Whatever, I my muscles are still sore, and because that isn’t annoying enough, I went cycling this evening, which was still very nice. Tomorrow I might ironically have switched out my sore legs for sore arms. Aperopos cycling, I need to fix my single speed bike because apparently I have to wait for the trams on the way back from ballet lesson rather long.

On Friday, I had another meeting with my supervisor. She had printed out all of my 20 pages I have so far (that’s including the title page, table of content etc. and about 10 pages of quotes and another two with pictures... Sooo I have written about 5? ooopsies). Like the last times, she only had constructive critism and suggestions for improvement. Also, I spontaneously decided to postpone my defense because she is on vacation exactly for the two weeks prior the old date and so she would have to read it there and I’m not that much of an asshole. Also, I want to do the topic justice as good as I can, so the three weeks more are very useful. 

Of course, I forgot my clever plan to ring the university for the document because I and my study buddies went to the canteen afterwards and then to the working room in our faculty, where I was not entirely unproductive but jotted down several questions. Now I just need to answer them, which is what I am currently trying to do. But since I am also watching Star Trek (the new-ish movies, also watching a film now is kinda possible again thanks to the later due-date), I would not get my hopes up too high. Also, man, Coxeter, why did you write so damn complicated? Why are you leaving out so many important facts and merely imply them? Very uncool. 

Hopefully, I will be more productive tomorrow, where we also will meet to go to the Datsche. Always wanted to go there but only walked past it once. It’s a bit out, so better get my bike fixed tomorrow morning. But then, will I get shit done for uni? Urgh. We’ll see. 

Here’s A Fast Way To Solve The Stretching Problem

We develop a strong stretching approximation for a polymer brush fabricated from self-avoiding polymer chains. Furthermore, in section IV, we put the brand new predictions to a test with simulation data on polymer brushes at very low grafting densities such that results of finite extensibility can be ignored. Only supreme chain models have been assumed in earlier literature for the analytic self-consistent calculation of the polymer brush density profile and the distribution of free ends. POSTSUBSCRIPT is measured from the BFM simulations of a single free chain on the corresponding chain lengths. Particularly, the predicted adjustments within the density profile and the free end distribution are elementary for understanding the compression behaviour of brushes, the interpenetration of two opposing brushes, or the relaxation of chains inside a brush. Likewise for the rotation kind instabilities, rotation about one cubic axis results in a tetragonal construction, about two orthogonal axes results in an orthorhombic part. FLOATSUBSCRIPT is displaced inside its surrounding octahedron, and antiferro-electric distortions, in which the octahedra rotate, presumably about a number of axes. The Steam Deck is a full-dimension controller with a 7-inch LCD touchscreen in the center; it has huge, rounded grips, haptic trackpads on both side of the display, and analog sticks and face buttons above those.

Frefsec:TBM, we describe the tight-binding methodology and parameters; the analog of Bloch waves in nanotubes; and the consequent methodology of perfectly matched layers to check defects. This paper applies a symmetry-tailored method to examine the influence of deformation and defects on the electronic construction and band construction in carbon nanotubes. The principle motivation of this paper is to grasp way of life choices and model their connection to other indicators, corresponding to mental health, resolution making etc. One of these evaluation will depend on capturing related details about yoga exercise from the text at the appropriate degree of granularity- understanding the outcomes of lifestyle choices requires modeling the people’s motivation for partaking in these actions, their level of commitment. 2013) the place the stability evaluation is based on the identical 1D Eggers & Dupont (1994) equations but made dimensionless using totally different characteristic length and time scales. C from Eq. (27), which may be very concerned, we will as a substitute decide it using Eqs. 마사지포털 will be extra enjoyable with others, so search for group fitness opportunities. Peloton, an organization that is recognized for internet-connected indoor bikes, is a fairly fashionable (if pricey) tech choice with health professionals. Inspired by the infinite households of finite and affine root systems, we consider a “stretching” operation on general crystallographic root programs which, on the extent of Coxeter diagrams, replaces a vertex with a path of unlabeled edges.

POSTSUPERSCRIPT. Since we use Zobrist hashing (see Section 3.2), this operation takes only fixed time. In Section three we present the definition of the pairing outlined by Cassels on 2-Selmer groups of elliptic curves. Figure 5 the curves roughly fall onto each other. The prediction of Equation (29) is compared in Figure 2 with the predictions from Refs. The place to begin for our method is a model equation for the chain deformation. Our symmetry-adapted strategy builds on the target Structures (OS) framework introduced by James Jam (06), and developed further by Dumitrica, James and others DJ (07); Jam (06); DJ (10); ADE13b ; ADE13a . Following the strategy of Schulze et al. As it's described under, throughout our analysis in this paper, we examine a pattern of 25 Milky Way (MW) like galaxies with the following frequent options. She also recommends utilizing ice on the aching space, stretching and taking anti-inflammatory remedy (like Advil® or Motrin®). To be able to decrease the time and resources required to prove our results, we perform the computations utilizing a binary integer illustration.

When you had the chance, would you pay more in order to use an exercise bike less? An additive quadratic strain gradient term within the energy density can be used as a proxy for the upper order (non-classical) elasticity of the pantographic frame. This shows that the off-centering and associated rhombohedral distortion lowers the power significantly extra efficiently than the octahedral rotation. The lone-pair chemistry is said to the off-centering. N being the variety of picture unit cells that might be both infinite or finite, the system above provides us an outline of the whole construction. 1111 for the perovskite structure to be stable. The cubic perovskite construction is well-known from the oxide perovksites to exhibit numerous doable part transitions. Thus, 3D factors are categorized as involved with the thing if they exhibit sufficiently high curvature in either route. Different tactile sensors enable a robot to make various vital measurements whereas in touch with an object, reminiscent of contact space, power, texture, and slip detection. The parallel-jaw gripper varies the stiffness of the membrane by uniaxially stretching it, which controllably modulates StRETcH’s effective modulus from approximately 4kPa to 9kPa. This work uses StRETcH to reconstruct the contact geometry of inflexible and deformable objects, estimate the stiffness of 4 balloons full of different substances, and manipulate dough into a desired form.

Cominiscule Posets

This post represents the first half of a talk given by Emine Yildirim at our combinatorics seminar.

You do not need to read the pre-talk post that I wrote to understand this one, but it would allow for a somewhat gentler introduction to the Coxeter transformation. The setup will use a lot of Coxeter groups language, but if you’re not familiar with it, you can literally just skip the first section without any loss of comprehension.

------ 

Turn Down for Theory

Let $W$ be a Coxeter group having a crystallographic root system $\Phi$ with highest root $\gamma$. Since the simple roots form a basis, we can write the highest root as a linear combination of the simple roots $\gamma = \sum c_i\alpha_i$.

We are now a stone’s throw from defining the words in the second half of the title:

Definition. A simple root is called cominiscule if $c_i=1$, and the (maximal) interval $\{\beta: \alpha_i\leq\beta\}$ in the root poset is called a cominiscule poset if $\alpha_i$ is cominiscule.

This is an abstract definition, but we because the Coxeter groups have a complete classification, we can also just write down all possible cominiscule posets.

In one of the previously-linked posts, we explicitly calculated which roots are cominiscule:

In type A, every root is cominiscule

In type C, only one root is cominiscule. (We will not consider type B, because the Coxeter groups associated to types B and C root systems are the same.)

In type D, three roots are cominiscule.

The only exceptional groups which have cominiscule roots are $E_6$ and $E_7$.

From these descriptions it is not hard straightforward to draw every possible cominiscule poset. And while the proofs of the theorems will definitely rely on the Coxeter theory, the rest of the talk only cares about the posets.

------

Meet the Posets

We now aim to write down a representative example of the cominiscule posets of types A, C, D, and also the only two cominiscule posets of type E. 

Since type A has so many cominiscule roots, we will draw the entire root poset first, just so that you can see where they come from. So, to be clear, only the bottom three pictures, with circled smallest element, represent cominiscule posets of type A.

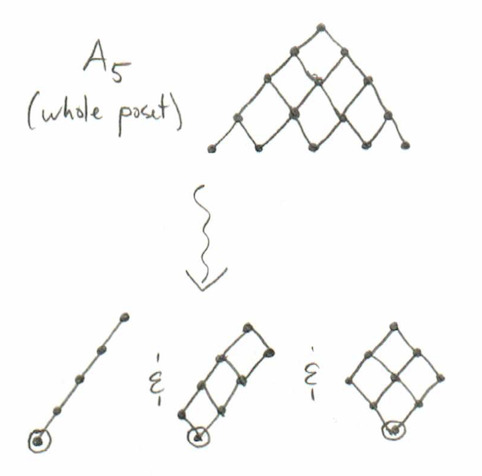
(You may be concerned that we didn’t use the roots on the “right side” but notice that the only thing this would do is reflect the posets across the vertical line. Those would still give the same order relations, so we only write the poset down once.)

Two of the cominiscule roots in type D give the same poset, and actually these also give the same poset as the only cominiscule root in type C:

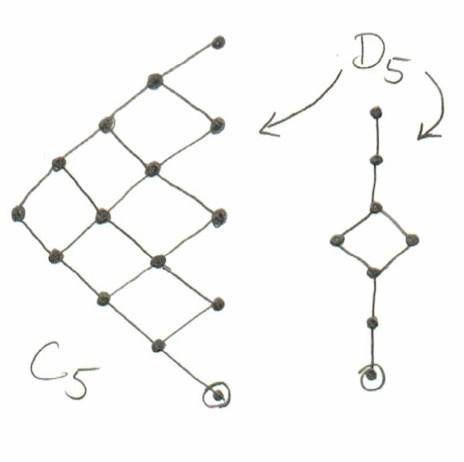
[ Amusingly, the shape of the cominiscule posets of type C always looks like the entire root poset of type A “rotated 90 degrees”. I think this is a coincidence; I would be surprised if there is a good theoretical explanation for this. ]

Finally, to round things out, here are the two type E posets:

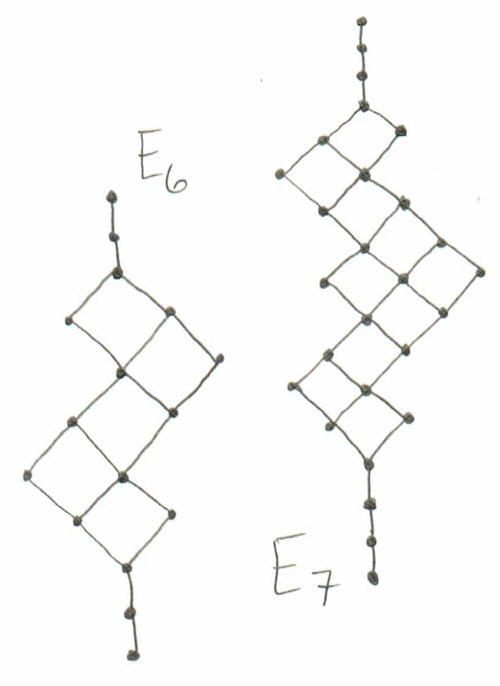
[ $E_6$ has two cominiscule roots, but they give rise to the same poset. ]

Now we have a bunch of posets to play around with. The natural question is, what are we going to do with them? The answer is algebra! and we’ll discuss that in the next post.

[ Previous ] [ Post 2 ] [ Next ]

Nerd sniping, by XKCD.

It could be that the author was inspired by a story from John H. Conway. According to Conway, Coxeter once nearly succeeded in murdering him. The murder weapon was a mathematical problem! Coxeter once came to Cambridge, gave a lecture, and ended with an open question in group theory. Conway left the lecture room thinking. Suddenly the idea hit him—while in the middle of the road. Conway stopped and a large truck ran into him, bruising him considerably. He limped back to the lecture room after the accident and joked that Coxeter had calculated the difficulty of the problem so precisely that he would get the solution just in the middle of the road. Eventually, Conway’s solution became a joint paper, and ever since, he’s called that theorem the murder weapon.

This shape is a small dodecicosahedron. It has twelve decagons in red, and twenty hexagons in five different colours. It was not documented until 1954 when HM Coxeter published his paper “Uniform Polyhedra”.

A knowledge of group theory can help when making shapes like this. It turns out that the colour arrangements around the twelve stars are based on the even permutations of four colours. This allowed me to quickly write down the valid colour arrangements, and then construct the star shaped sections in advance. This is more efficient and less error prone than trying to deduce the colours on the fly during assembly.

As usual, it was fun but time consuming to make.

What is a coxeter group dual to?

i dunno anon, what is a coxeter group dual to?

There are no theorems in category theory.

Emily Riehl, Category Theory In Context

Mathematicians often tell her this; hence the book.

If I had to summarise her views in one sentence, it would be:

Everything is an adjunction.

I also like the division these mathematicians are making to her: essentially, a theorem is anything that solves Feynman’s challenge: by a series of clear, unsurprising steps, one arrives at an unexpected conclusion.

Examples for me include:

17 possible tessellations

6 ways to foliate a surface

27 lines on a cubic

1, 1, 1, 1, 1, 1, 28, 2, 8, 6, 992, 1, 3, 2, 16256, 2, 16, 16, 523264, 24, 8, 4 ways to link any-dimensional spheres.

the existence of sporadic groups

surprising rep-theory consequences of Young diagrams, Ferrers sequences, and so on (you could say the strangeness of integer partitions is really to blame here…)

59 icosahedra

8 geometric layouts

Books which are bristling with mathematical ideas of this kind include Montesinos on tessellations, Geometry and the Imagination (the original one), and Coxeter’s book on polyhedra (start with Baez on A-D-E if you want to follow my path). Moonshine and anything by Thurston or his students, I’ve found similarly flush with shockng content—quite different to what I thought mathematics would be like. (I had pictured something more like a formal logic book: row by row of symbols. But instead, the deeper I got into mathematics, the fewer the symbols and the more the surnames thanking the person who came up with some good idea.)

Note that a theorem is different here to some geometry — as in The Geometry of Schemes. The word geometry used in that sense, I feel, is to have a comprehensive enough vision of a subject to say how it “looks” — but the word theorem means the result is surprising or unintuitive.

This definition of a theorem, to me, presents a useful challenge to annoying pop-psychology that today lurks under the headings of Bayesianism, cognitive _______, behavioural econ/finance, and so on.

Following Buliga and Thurston to understand the nature of mathematical progress, within mathematics at least (where it’s clearer than elsewhere whether you understand something or not—compare to economic theory for example), there is a clear delination of what’s obvious and what’s not.

What is definitely not the case in mathematics, is that every logical or computable consequence of a set of definitions is computed and known immediately when the definitions are stated! You can look at a (particularly a good) mathematical exposition as walking you through the steps of which shifts in perspective you need to take to understand a conclusion. For example start with some group, then consider it as a topological object with a cohomology to get the centraliser. Or in Fourier analysis: re-present line-elements on a series of widening circles. Use hyperbolic geometry to learn about integers. Use stable commutator length (geometry) to learn about groups. Or read about Teichmüller stuff and mapping class groups because it’s the confluence of three rivers.

Sometimes mathematical explanations require fortitude (Gromov’s "energy") and sometimes a shift in perspective (Gromov’s (neg)"entropy").

This view of theorems should be contrasted to the disease of generalisation in mathematical culture. Citing two real-life grad students and a tenured professor in logic (one philosophical, one mathematical, the professor in computer science):

I like your distinction between hemi-toposes, demi-toposes, and semi-toposes

I care about hyper-reals, sur-reals, para-consistency, and so on

Abstract thought — like mathematicians do — is the best kind of thought.

(twitter.com/replicakill, the author of twitter.com/logicians, ragged on David Lewis by saying “What do mathematicians like?” “What do mathematicians think?” —— And Corey Mohler has done a wonderful job of mocking Platonism, which is how I guess the thirst for over-generalisation reaches non-mathematicians.)

Paul Halmos knew that cool examples beat generalisations for generalisation’s sake, as did V. I. Arnol’d. And it seems that the people a Harvard mathematician spends her time with make reasonable demands of a mathematical idea as well. It shouldn’t just contain previous theories; it should surprise. In Buliga’s Blake/Reynolds dispute, Blake wins hands down.

Siobhan Roberts, King of Infinite Space: Donald Coxeter, the Man Who Saved Geometry, Appendix 4: Coxeter Group, Walker & Company, New York, NY, 2006, pp. 263-264

The word problem for Pride groups

(1)The word problem for Pride groups Peter Davidson Department of Mathematics & Statistics, University of Strathclyde, Glasgow G1 1XH, United Kingdom. [email protected] Abstract Pride groups are defined by means of finite (simplicial) graphs and examples include Artin groups, Coxeter groups and generalized tetrahedron groups. Under suitable conditions we calculate an upper bound of the first order Dehn function for a finitely presented Pride group. We thus obtain sufficient conditions for when finitely presented Pride groups have solvable word problems. As a corollary to our main result we show that the first order Dehn function of a generalized tetrahedron group, containing finite generalized triangle groups, is at most cubic. 2000 Mathematics Subject Classification: 20F05, 20F06, 20F10 1 Introduction An Artin group has a presentation of the form ha1, a2, . . . , an;aiajai. . . | {z } µij =ajaiaj. . . | {z } µji for all i6=ji, where µij = µji is an integer greater than or equal to 2 or µij = ∞, in (2)groups include free groups, free abelian groups and braid groups. Indeed Artin groups are sometimes referred to as generalized braid groups, the latter introduced explicitly by Emil Artin in 1925. It is unknown in general whether or not Artin groups have solvable word problems, however some partial results do exist. If we add the defining relation ai =a−i 1 for each i= 1, . . . , n then we obtain the corresponding Coxeter group ha1, a2, . . . , an;a2i = 1,(aiaj)µij = 1 for all i6=ji and we say that an Artin group is spherical (or offinite type) if its corre-sponding Coxeter group is finite. The word problem is solvable for spherical Artin groups (see [7] and [4]). The word problem is also solvable for right-angled Artin groups, where µij = 2 for all i 6= j. If µij ≥ 3 for all i 6= j then the Artin group is said to be oflarge type. Following joint work with Schupp, Appel [2] showed that such groups have solvable word problems. Finally, Altobelli [1] proved that Artin groups of FC type have solvable word problem. Artin groups of FC type can be characterized as the small-est class of Artin groups which is closed under free products amalgamated over special subgroups and which contain spherical Artin groups. Artin groups, and their corresponding Coxeter groups, are but two ex-amples of a much wider class of groups. Notice that in each of their pre-sentations the defining relations involve at most two generators. Finitely presented groups that have such presentations were first studied by Pride in [12] and later in [15] under the title “groups given by presentations in which each defining relator involves at most two types of generators.” It is common to refer to such groups as simplyPride groups. Let Γ = {V, E} be a finite simplicial graph with vertex set V and edge set E. To each vertex v ∈ V assign a group Gv with a fixed finite

https://1library.net/document/dzxx33nz-the-word-problem-for-pride-groups.html

Well damn.  Turns out a bunch of the Twiztor groups that I thought were also Coxeter groups are not in fact Coxeter groups.

Delta Green: Bestow

A group of untested agents have been asked to assist a rare book dealer who appears to be suffering from a mental breakdown. However, the dealer has fled into the Coxeter Museum, a small art museum and gallery. When the team enters the building, it quickly becomes apparent that the building’s interior is unlike any other structure they have ever encountered. It is a maze beyond their wildest…

View On WordPress