#bisector's | Explore Tumblr Posts and Blogs

ebqzpnhcvim · 1 year

Text

Hubby Fucking My Pussy Hard My girlfriend big tities Car and home sex Malaysian gurl Teen outdoor first time xxx My dad has always told me that keeping Bangalore neighbour aunty fucking me Babes - Aural Pleasure starring Layla Rose and Natalia Starr Blondie and Antonella Del Lago in a lesbian scene Tattoo big booty dildo in the shower Chloe Carter puts a cock in her mouth

0 notes

bio-metal404 · 4 months

Text

Random ass color edits I never showed in world LOL

I like the scrapped and non canon reploids

#+ kill me lol i like more the old version of zero #my edit #mega man x #mega man x navigator #concept art edit #mega man x irregular hunter #mega man x heel #mega man x zero #the navigator i call Bissectrisa in Russian it's mean Bisector #and the tall mechanic as Clock the short one as Tock the middle as Occur lol #i should draw them soon or something #(mmx)heel #concept art navigator

7 notes · View notes

werchezdeeno · 1 year

Text

cinnamoroll drinks younger shinonome coffee

i am bored

#shinonome akito #akito shinonome #dang akito bisector fr #hand of akito #vivid bad squad #project sekai #cinnamoroll #sanrio #cute #ig #i mean cinnamoroll is #akito tho #in toya's opinion #he is #so tag stays true #toya aoyagi #hhh and not jade #my edit

20 notes · View notes

littlemuoi · 9 months

Text

#brf #royal anecdote #THE MAGICAL BISECTOR #MUAHAHAHAHAHA #THIS IS NUTS #ed #peter phillips #chuck #prince edward #duke of edinburgh

8 notes · View notes

gayofthefae · 2 years

Text

You were being a total douche to El, all day.

El needs you Mike, and she always will.

#stranger things #byler #this isn't a triangle it's a line and she's the bisector #not to be confused with the bisexual

29 notes · View notes

electricpurrs · 1 year

Text

found out the original my bisexual wife post is gone and so seems to be the artists blog, ive never been sadder in my life

#people keep making posts reposting the bisexual wife painting and i was gonna link up the original post from the artist blog #but it seems to be gone #i wonder what happened to them.....#edit. how the hell did it correct bisexual to bisector #i hate this phone

7 notes · View notes

winchesterwitch07 · 2 years

Note

I haven't talked to you in awhile so I decided to send you some flowers

aw it's gorgeous love

here's a cool rock for you <3

#the bisector

7 notes · View notes

lume-nosity · 2 years

Text

uhhh does anyone know how to solve angle & perpendicular bisectors?

i kinda got the gist of it (as i went through notes and watched videos) but i need it to be re-explained to me as if im a toddler

if you’re that person who saw this and went: ‘oh this shit’s easy’ then can you do me a favor and tell me how to solve them in simple words please,,math isn’t my expertise

pls help i beg

#☁️ lume speaks #studyblr #math #algebra #school #geometry #hw #geometry quiz #quiz #homework #angle bisectors #perpendicular bisectors #this is a cry for help #i don’t want to fail my first math quiz of the year :sob:

1 note · View note

squareallworthy · 3 hours

Note

Reverse unpopular opinion ask meme: Irregular polygons

Irregular polygons are awesome. You can do so much more with them, in so many areas, but I'm going to limit myself to talking about just two of them: tiling and triangle centers.

(Did you think I was going to be all snobby toward my irregular friends and give them only grudging approval? Heck no, I love those guys! And so by the rules of the meme I get to infodump about the things I love, so this may be long but you asked for it.)

Let's first talk about covering the plane with copies of a single shape -- a monohedral tiling. And for now, let's restrict ourselves to periodic tilings. All triangles and all non-self-intersecting quadrilaterals tile the plane periodically, so that's not very interesting. All you have to do is place one polygon and then make copies by rotating 180 degrees around the midpoints of the sides.

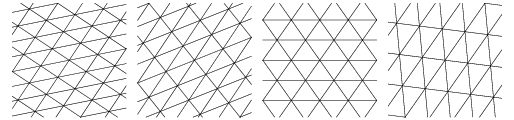
With five sides, things become more complicated, because regular pentagons don't tile by themselves, but there are fifteen ways an irregular pentagon can periodically tile the plane. Here are four of them that were discovered in 1976 and 1977 by Marjorie Rice, an amateur mathematician.

There are three types of monohedral periodic convex hexagonal tilings.

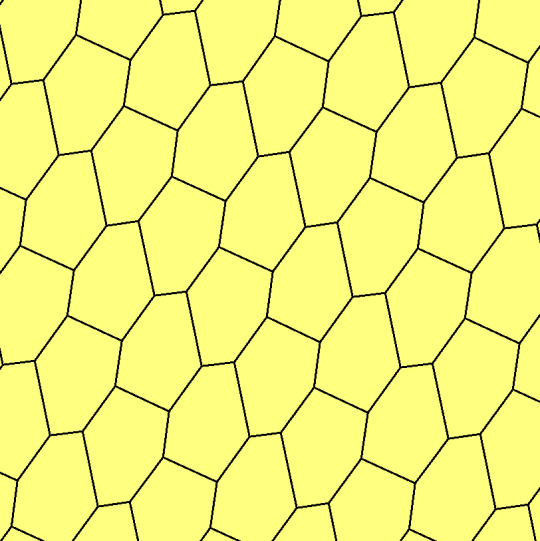
For polygons with seven or more sides, there are no monohedral periodic tilings using a convex prototile , but there are periodic tilings for nonconvex polygons of any size. Some of them are quite famous.

Most of Escher's work in his Regular Division of the Plane series uses shapes with curves as well as straight sides, so they don't show polygon tilings, strictly, but the patterns do point toward complex tilings that are visually pleasing.

Irregulars can tile aperiodically, too. Here's a pentagon tiling with 6-fold rotational symmetry. It can be extended infinitely, and tilings can be constructed with pentagons for n-fold symmetry of any n>2.

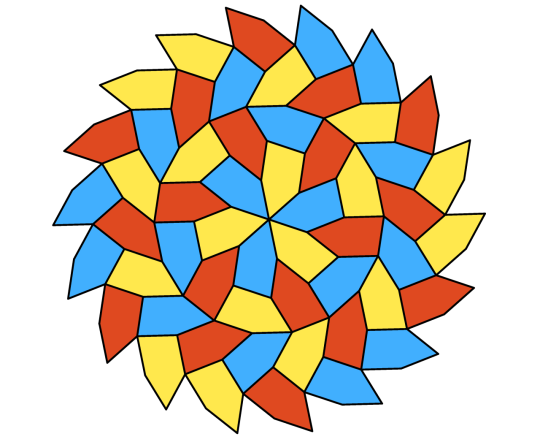
Going back to non-convex shapes, here's the Voderberg tile, an enneagon that forms a spiral tiling. Notably, one copy of the shape can be completely surrounded by two others.

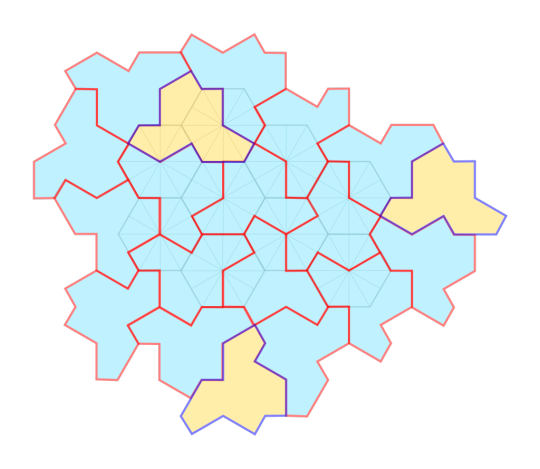
And of course I can't go without mentioning the tiling news of the century: "Tile (1,1)", aka the Hat, aka the T-shirt, a tridecagon (and polykite) that can tile the plane but only aperiodically. IDK if you follow polygon news but this was huge.

Okay, enough about tilings. With tilngs it's pretty easy to get what's going on just by looking at them, but my next topic, triangle centers, requires a bit more explanation. Also there's a bit of jargon, but I will try to keep it simple.

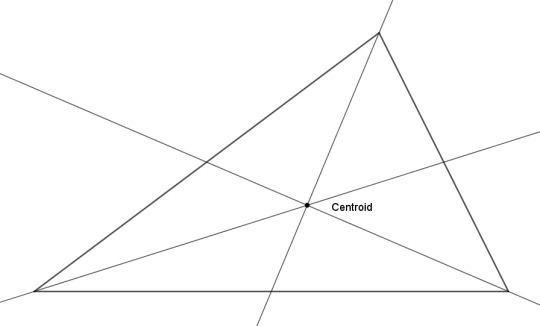
Take an arbitrary triangle ABC. Where is its center? One way you might define it is to find the midpoint of each side and draw a line to it from the opposite vertex. Each line divides the triangle in half, and these three lines (the medians) all cross at a point, the centroid. This works for any triangle, no matter its shape. The point marks the center of gravity of the area of the triangle, and also the center of gravity of its vertices. Based on that, you could consider this the center of the triangle.

Or you could work with angles instead of sides. Draw lines from each vertex that divide the angles in half (the angle bisectors). These all meet at a point called the incenter, which marks the center of the largest circle that fits inside the triangle. To put it another way, it's the point that is equidistant from all three sides. That's another point you could call the center of the triangle.

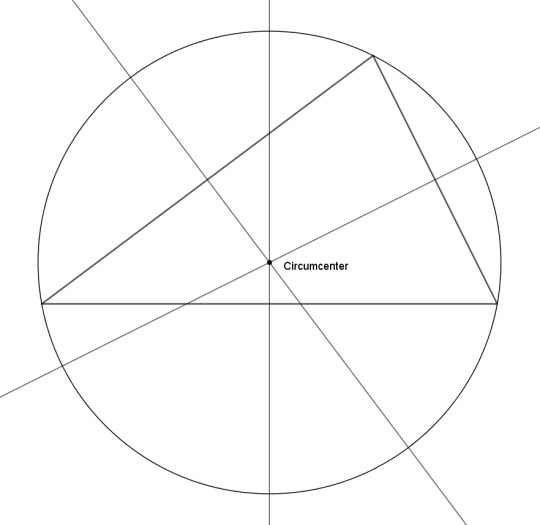
Or, how about a circle around the triangle instead? From the midpoints of the sides, draw the perpendicular bisectors. Again, they all intersect at a point, the circumcenter, which is the center of the circle that passes through the vertices -- the point that is equidistant from all three of them. So you could also call that the center of the triangle.

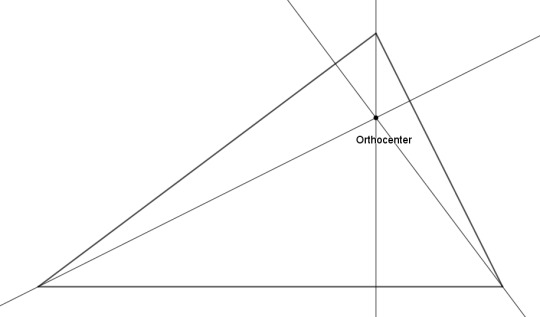
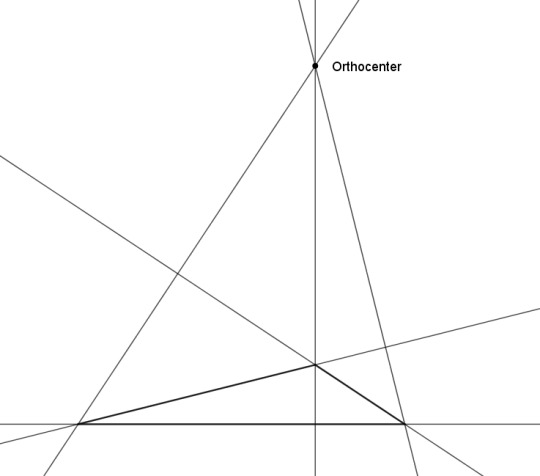
Or how about drawing perpendicular lines from the sides again, but having them pass through the opposite vertices (the altitudes)? They coincide at a point called the orthocenter. Isn't that neat? Yet another point we could call the center of the triangle.

But wait -- can we? For an obtuse triangle, the circumcenter and the orthocenter are going to lie outside the triangle. (For the orthocenter of an obtuse triangle, you have to extend each side into a line, and draw the altitude as a perpendicular to that.) Being outside a thing is really not what we have in mind when we talk about the center of the thing. Should we care about that?

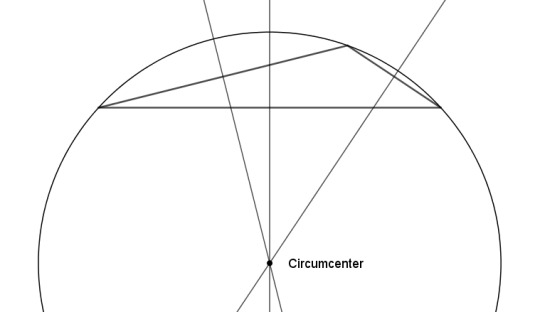
Maybe not. Check this out. We'll go back to the circumcircle, and draw tangents to it at the three vertices. The three tangents form the tangential triangle (in blue), which we'll call A'B'C', where A' is opposite A, and so on with B and C. Now draw the circle that passes through A, A', and the circumcenter, and do the analogous construction for B and C (in red). The three circles coincide in two places: the circumcenter and another point called the far-out point. And as the name suggests, this is usually well outside the triangle, even for acute triangles.

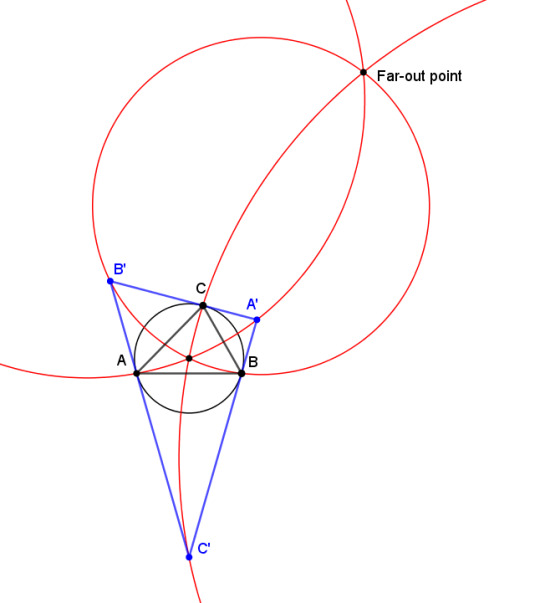
There's no reasonable way to call this point the center of the circle. But so what? I just love the fact that the three circles line up like that. I no longer care about finding "the" center of the triangle. I no longer care that "center" is rather a misnomer for many of these points. I just think it's neat that you can draw these constructions on ordinary aysmmetrical triangles and they keep all converging on one point. Want more? Reflect the medians across the angle bisectors, and they all meet at the symmedian point. Or connect the vertices of the tangential triangle with the intersections of the medians and the circumcircle. Those lines meet at the Exeter point. Or, from each vertex, draw the line that splits the perimeter of the triangle in half. These are called the splitters, and they meet at the Nagel point. And on and on and on.

You can simply wander around a triangle, connecting things that relate somehow to vertex A, then do the equivalent thing for B and C, and stumble upon new centers. And there are tens of thousands of these things, constructed with straightedge and compass or by other methods. And there are so many ways to enjoy these things. You can page through the enormous collection and get a kind of stamp-collecting satisfaction just looking at their variety and knowing that they exist. Or you can appreciate the proofs that show that the constructions really do specify a unique point. Or proofs that show that a point constructed to have one property has a surprisingly different property. Or you can notice that the points fall into certain families and appreciate the connections between them. (For instance, the centroid, circumcenter, orthocenter, far-out point, and Exeter point, among others, all happen to lie on the same line, the Euler line.) Or you can convert the points to trilinear coordinates, manipulate them algebraically, and get to know them that way.

But to appreciate them at all, you need to work with irregular triangles. Because here's the thing: in an equilateral triangle, all these points collapse to the same point. Everything simplifies to a single center, and the incredible wealth of invisible structure that teems inside every ordinary triangle is gone.

You have finally found "the" center, but at what cost? Symmetry is death. Only through asymmetry will the vast truth of the triangle be revealed to you.

And those are just a few of the reasons irregular polygons are cool!

#polygon representation

29 notes · View notes

skronklpus · 17 days

Note

hi, I had a question. On your Jax art there are Spanish lyrics(?) In the background. I was wondering what song it was? Or where it's from? Sorry I'm just curious. Absolutely love the art

Thank you ! I’m so happy you like the art and that you’re curious about the song - it’s called “Así Soy Yo “ (That’s How I am )

by El Cuarteto de Nos

Here’s the translated lyrics if you’re interested:

I have no pains, I have no loves

And thus I don't suffer disappointments

With the whole world I'm even

Since I don't play, I neither lose nor win

I don't have much, neither do I have little

Since I don't give an opinion, I'm never wrong

And since I don't set goals for myself

I've never known failure

Happiness and sadness are the same to me

Because I don’t care to feel

Because in the angle of life

I have decided to be the bisector

Ohhh, that's how I am

I don't bother to get a partner

That way I don't suffer when they leave me

I have never loved anyone seriously

So I never cry at funerals

Nothing happens if I don't move

That's why I don't care about anything

And indecision doesn't kill me

If "should I stay, or should I go"

Eyes that don't see, heart that doesn't feel

It’s what a blind cuckold once said

And I'm not like Hamlet Perez

I don't care at all about to be or not to be

Ohhh, that's how I am

Some will just say, "Oh how insensitive"

And others say "How empty and plain"

And those words are gone with the wind

Since I don't listen , I don't get mad

I'm neither up nor down

I don't get better, nor will I get worse

And since I never start anything

I don't get anxious about getting it done

Ohhh, that's how I am

#el cuarteto de nos

21 notes · View notes

nukebag · 6 months

Text

he’s gonna draw the perpendicular bisector of a line and you can’t stop him!! >:)

#star wars clone wars #clone trooper #arc trooper jesse #clones #clone troopers #tcw #501st legion #i’m hilarious i know

50 notes · View notes

study-with-aura · 3 months

Text

Tuesday, March 19, 2024

My mom got me a bunny! I named her Sherbet because she sort of reminds me of sherbet. I went through several names however. At first it was Bun-Bun and then Hop-Hop and then BeBe and then Poppy, and then I think I finally settled on Sherbet. I will let you know if I change my mind again. Isn't she cute though?

The study day went by quickly. I didn't need my full four hours, so I added in a supplement for Biology since we're on the evolution unit right now. My curriculum is mostly a creationist perspective, although it touches on evolution and natural selection, so I found this docuseries called Life on Our Planet which dives deeper into evolution. I don't need my parents permission to watch the docuseries since they give me a lot of freedom around things like that, but I still let them know I was going to. Apparently my dad has already seen it, and he thought I would enjoy it. That was a surprise to me that he had watched it. The first episode was suspenseful, but I am looking forward to watching more. I will have to build it into my study day somehow. I think it has 10 episodes, all a little under an hour long.

Tasks Completed:

Geometry - Learned to construct perpendicular bisectors and angle bisectors + practice + practice with proofs involving segments and angles + honors work

Lit and Comp II - Reviewed Unit 21 vocabulary + read chapter 39 of Emma by Jane Austen

Spanish 2 - Vocabulary test (100%)

Bible I - Read Judges 12-13

World History - Read second part of the introduction to the unit + read about Albert Einstein + read about Pablo Picasso + viewed some of Picasso's artwork

Biology with Lab - Read and watched videos on the functionality of life from a creationist perspective

Foundations - Read the definition of self-control + completed next quiz on Read Theory + read an article about propaganda in schools

Piano - 60-minute piano lesson + practiced for one hour

Khan Academy - None today

CLEP - None today

Streaming - Watched episode 1 of Life on Our Planet (evolutionist perspective)

Duolingo - Studied for 15 minutes (Spanish, French, Chinese) + completed daily quests

Reading - Read pages 177-226 of House of Salt and Sorrows by Erin A. Craig

Chores - Laundry

Activities of the Day:

Personal Bible Study (Colossians 3)

Ballet

Pointe

Journal/Mindfulness

-

What I’m Grateful for Today:

I am grateful that my parents agree and encourage me to study the beginnings of life from creationist and evolutionist perspectives instead of only creationism.

Quote of the Day:

Every act of creation is first of all an act of destruction.

-Pablo Picasso

🎧Suite in B minor for piano, op. 58 - Charles-Marie Widor

#study blog #study inspiration #study motivation #studyblr #studyblr community #study community #study-with-aura

16 notes · View notes

taringill · 4 months

Text

Hazbin Hotel mem

Видео взято с канала INKLING на YouTube. Видео называется "Мемы по Отелю Хазбин / 4 часть". Решила поделиться, в первый раз я так смеялась😅 Мне понравилось

The video is taken from INKLING's YouTube channel. The video is called "Мемы по Отелю Хазбин / 4 часть". I decided to share it, the first time I laughed so much😅 I enjoyed it

Translation, if someone needs it

Velvette: Am I a baby?!

Vox: Yeah. I'm 800-some dick years old

Valentino: Dicks are good) Do you have a big one?

Vox: Yes))

Valentino: How much?

Vox: 4 by 4

Velvette: Is it a square?

VVV: *laughing*

Vox: The fucking rectangle. AHHAHA

Valentino: You need to suck dicks, not find perimeters in them

VVV: *laughing*

Vox: What's yours?

Velvette: The fucking triangular

Vox: HAHA

Valentino: Is it also necessary to calculate the bisector before sucking?

VVV: *laughing*

#mem #hazbin hotel #hazbin hotel memes #hazbin hotel vvv #hazbin hotel velvette #hazbin hotel vox #hazbin hotel valentino

15 notes · View notes

staaar-an · 3 months

Text

(˶ᵔ ᵕ ᵔ˶)

⊹ Have you seen what a sad letter from my beloved this year? 🥺

⊹ He's become so serious that I'm going to turn into a bisector right now

#genshin impact #digitalart #artists on tumblr #digital #Bennett #genshin impact bennett

9 notes · View notes

mathhombre · 8 months

Text

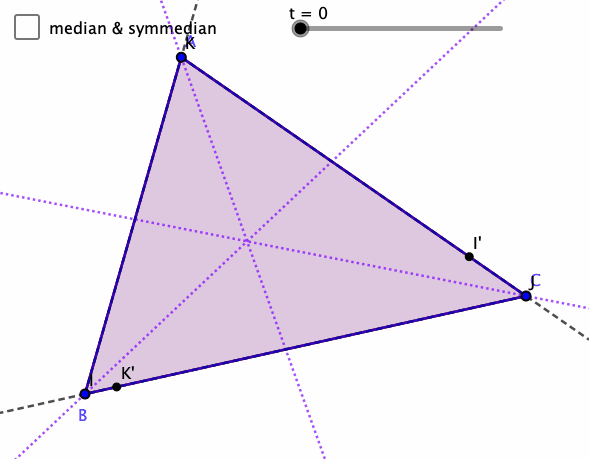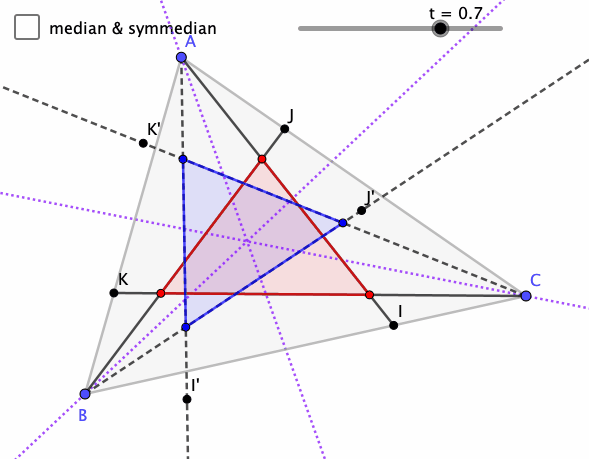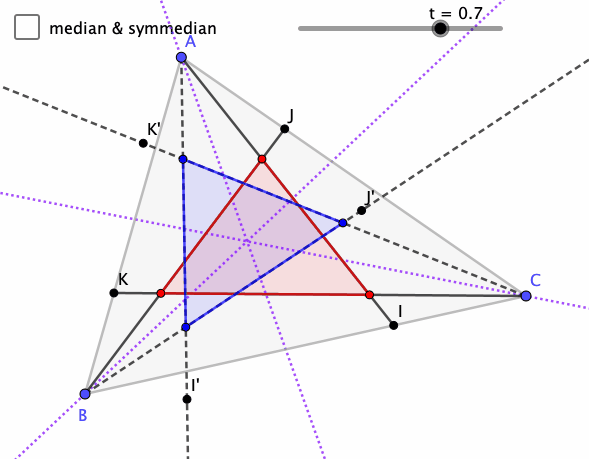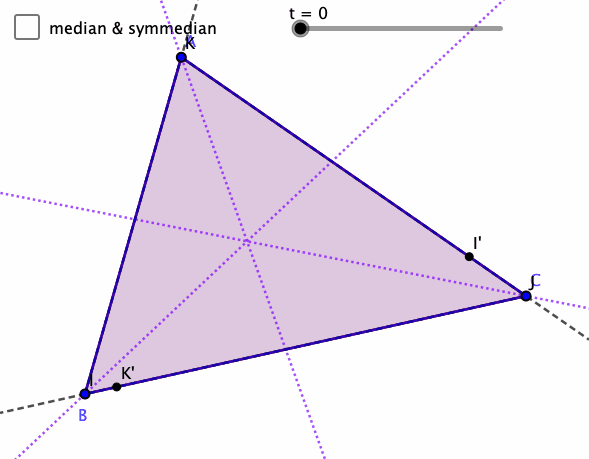
Symmedian

Day 2 of Mathober is Symmedian.

Had to remind myself what that means, the reflection of the median across the angle bisectors (isogonal to the medians). And just like the medians are concurrent, then so are the symmedians, and their intersection is the isogonal conjugate to the centroid (the intersection of the medians).

There's an idea called the trilinear coordinates for a point in a triangle, and the trilinear coordinates for the symmedian intersection are the inverse of that for the centroid. I'm not sure how to produce the trilinear coordinates given a point, nor find a point from the trilinear coordinates. There's always more to learn.

This sketch generalizes the median to the corresponding points parameterized by t, and those segments isogonal segments. Pretty fascinating to me.

What do you notice and wonder?

Sketch is on GeoGebra.

#GeoGebra #Mathober

8 notes · View notes

coern · 7 months

Text

I don't know how to do my science work(I thought I'd ask for my father's help) but I got glared at for listening to music and drawing and not doing my work(that I don't know how to do) so I'm sitting here, tears in my eyes, constructing angle bisectors because its oddly charming as an activity for boredom while a girl watches cocomelon or something next to me

#this is like an entire mobile game for me #my post

5 notes · View notes