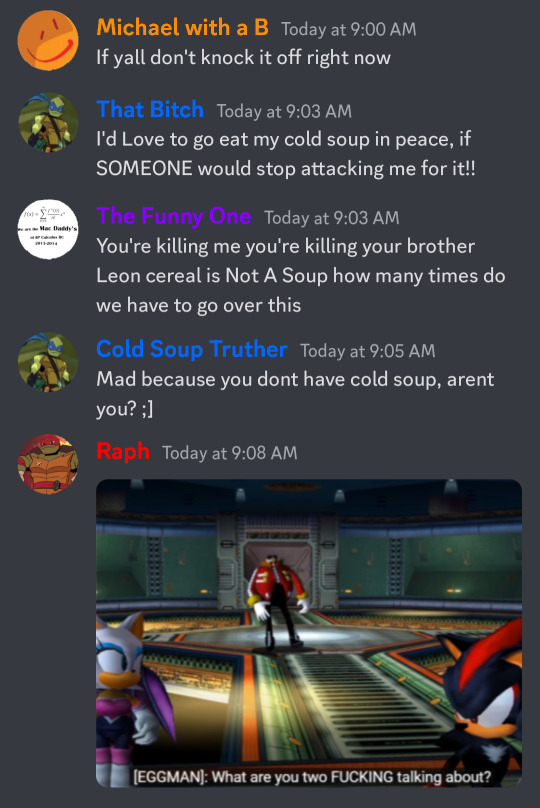
[ID: fake discord screenshots between the tmnt boys. The chat reads as follows, with their discord nicknames in parentheses:

Mikey (Micheal with a B): If yall don't knock it off right now

Leo (That Bitch): I'd Love to go eat my cold soup in peace, if SOMEONE would stop attacking me for it!!

Donnie (The Funny One): You're killing me you're killing your brother Leon cereal is Not A Soup how many times do we have to go over this

Leo changes his name to "Cold Soup Truther"

Leo (Cold Soup Truther): Mad because you dont have cold soup, arent you? ;]

Raph sends a screenshot from the sonic realtime fandub of Eggman saying "what are you two FUCKING talking about"

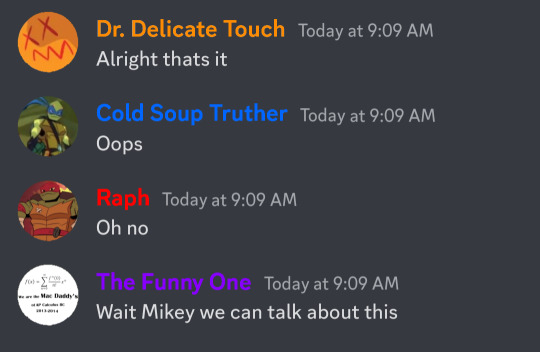
Mikey's name changes to "Doctor Delicate Touch"

Mikey (Doctor Delicate Touch): Alright that's it

Leo (Cold Soup Truther): Oops

Raph (Raph): Oh no

Donnie (The Funny One): Wait Mikey we can talk about this

End ID]

Laid awake for several hours thinking about wanting to make this joke the other day

Bonus: the aftermath

[ID: a simplistic drawing of the turtles. Mikey runs at high speed chasing Donnie and Leo, Raph lays behind him flat on the floor with x's for eyes. There are action lines emanating out from where Donnie and Leo are running to. End ID]

Test Bank For Calculus: Early Transcendentals, 12th Edition By Howard Anton

TABLE OF CONTENTS   PREFACE vii   SUPPLEMENTS ix   ACKNOWLEDGMENTS xi   THE ROOTS OF CALCULUS xv   1 Limits and Continuity 1   1.1 Limits (An Intuitive Approach) 1   1.2 Computing Limits 13   1.3 Limits at Infinity; End Behavior of a Function 21   1.4 Limits (Discussed More Rigorously) 30   1.5 Continuity 39   1.6 Continuity of Trigonometric Functions 50   1.7 Inverse Trigonometric Functions 55   1.8 Exponential and Logarithmic Functions 62   2 The Derivative 77   2.1 Tangent Lines and Rates of Change 77   2.2 The Derivative Function 87   2.3 Introduction to Techniques of Differentiation 98   2.4 The Product and Quotient Rules 105   2.5 Derivatives of Trigonometric Functions 110   2.6 The Chain Rule 114   3 Topics in Differentiation 124   3.1 Implicit Differentiation 124   3.2 Derivatives of Logarithmic Functions 131   3.3 Derivatives of Exponential and Inverse Trigonometric Functions 136   3.4 Related Rates 142   3.5 Local Linear Approximation; Differentials 149   3.6 L’Hoˆ pital’s Rule; Indeterminate Forms 157   4 The Derivative in Graphing and Applications 169   4.1 Analysis of Functions I: Increase, Decrease, and Concavity 169   4.2 Analysis of Functions II: Relative Extrema; Graphing Polynomials 180   4.3 Analysis of Functions III: Rational Functions, Cusps, and Vertical Tangents 189   4.4 Absolute Maxima and Minima 200   4.5 Applied Maximum and Minimum Problems 208   4.6 Rectilinear Motion 222   4.7 Newton’s Method 230   4.8 Rolle’s Theorem; Mean-Value Theorem 235   5 Integration 249   5.1 An Overview of the Area Problem 249   5.2 The Indefinite Integral 254   5.3 Integration by Substitution 264   5.4 The Definition of Area as a Limit; Sigma Notation 271   5.5 The Definite Integral 281   5.6 The Fundamental Theorem of Calculus 290   5.7 Rectilinear Motion Revisited Using Integration 302   5.8 Average Value of a Function and its Applications 310   5.9 Evaluating Definite Integrals by Substitution 315   5.10 Logarithmic and Other Functions Defined by Integrals 320   6 Applications of the Definite Integral in Geometry, Science, and Engineering 336   6.1 Area Between Two Curves 336   6.2 Volumes by Slicing; Disks and Washers 344   6.3 Volumes by Cylindrical Shells 354   6.4 Length of a Plane Curve 360   6.5 Area of a Surface of Revolution 365   6.6 Work 370   6.7 Moments, Centers of Gravity, and Centroids 378   6.8 Fluid Pressure and Force 387   6.9 Hyperbolic Functions and Hanging Cables 392   7 Principles of Integral Evaluation 406   7.1 An Overview of Integration Methods 406   7.2 Integration by Parts 409   7.3 Integrating Trigonometric Functions 417   7.4 Trigonometric Substitutions 424   7.5 Integrating Rational Functions by Partial Fractions 430   7.6 Using Computer Algebra Systems and Tables of Integrals 437   7.7 Numerical Integration; Simpson’s Rule 446   7.8 Improper Integrals 458   8 Mathematical Modeling with Differential Equations 471   8.1 Modeling with Differential Equations 471   8.2 Separation of Variables 477   8.3 Slope Fields; Euler’s Method 488   8.4 First-Order Differential Equations and Applications 494   9 Infinite Series 504   9.1 Sequences 504   9.2 Monotone Sequences 513   9.3 Infinite Series 520   9.4 Convergence Tests 528   9.5 The Comparison, Ratio, and Root Tests 534   9.6 Alternating Series; Absolute and Conditional Convergence 539   9.7 Maclaurin and Taylor Polynomials 549   9.8 Maclaurin and Taylor Series; Power Series 559   9.9 Convergence of Taylor Series 567   9.10 Differentiating and Integrating Power Series; Modeling with Taylor Series 575   10 Parametric and Polar Curves; Conic Sections 588   10.1 Parametric Equations; Tangent Lines and Arc Length for Parametric Curves 588   10.2 Polar Coordinates 600   10.3 Tangent Lines, Arc Length, and Area for Polar Curves 613   10.4 Conic Sections 622   10.5 Rotation of Axes; Second-Degree Equations 639   10.6 Conic Sections in Polar Coordinates 644   11 Three-dimensional Space; Vector   11.1 Rectangular Coordinates in 3-Space; Spheres; Cylindrical Surfaces 657   11.2 Vectors 663   11.3 Dot Product; Projections 673   11.4 Cross Product 682   11.5 Parametric Equations of Lines 692   11.6 Planes in 3-Space 698   11.7 Quadric Surfaces 705   11.7 Cylindrical and Spherical Coordinates 715   12 Vector-Valued Functions 723   12.1 Introduction to Vector-Valued Functions 723   12.2 Calculus of Vector-Valued Functions 729   12.3 Change of Parameter; Arc Length 738 12.4 Unit Tangent, Normal, and Binormal Vectors 746   12.5 Curvature 751   12.6 Motion Along a Curve 759   12.7 Kepler’s Laws of Planetary Motion 771   13 Partial Derivatives 781   13.1 Functions of Two or More Variables 781   13.2 Limits and Continuity 791   13.3 Partial Derivatives 800   13.4 Differentiability, Differentials, and Local Linearity 812   13.5 The Chain Rule 820   13.6 Directional Derivatives and Gradients 830   13.7 Tangent Planes and Normal Vectors 840   13.8 Maxima and Minima of Functions of Two Variables 845   13.9 Lagrange Multipliers 856   14 Multiple Integrals 925   14.1 Double Integrals 925   14.2 Double Integrals Over Nonrectangular Regions 932   14.3 Double Integrals in Polar Coordinates 941   14.4 Surface Area; Parametric Surfaces 948   14.5 Triple Integrals 961   14.6 Triple Integrals in Cylindrical and Spherical Coordinates 968   14.7 Change of Variables in Multiple Integrals; Jacobians 977   14.8 Centers of Gravity Using Multiple Integrals 989   15 Topics in Vector Calculus 1001   15.1 Vector Fields 1001   15.2 Line Integrals 1010   15.3 Independence of Path; Conservative Vector Fields 1025   15.4 Green’s Theorem 1035   15.5 Surface Integrals 1042   15.6 Applications of Surface Integrals; Flux 1049   15.7 The Divergence Theorem 1058   15.8 Stokes’ Theorem 1067   APPENDIX A A1   APPENDIX B 00   APPENDIX C 00   APPENDIX D 00   APPENDIX E 00   ANSWERS 00   INDEX I1         Read the full article

bernoulli would’ve won

Today I learned that Bernoulli numbers are p-adic integrals. TeX-heavy so click to read on.

First of all, Bernoulli numbers are traditionally defined as coefficients of the Taylor series $$ \frac{s}{e^s - 1} = \sum_{k=0}^\infty B_k\frac{s^k}{k!}. $$ We have $$B_0 = 1, B_1 = -\frac{1}{2}, B_2 = \frac{1}{6}, B_3 = 0, B_4 = \frac{1}{30}, $$ and $B_{2n+1} = 0$ for $n \ge 1$. I don’t have a cute slogan for what they mean, because they’re one of these sequences that shows up all throughout math: in calculating sums of powers of natural numbers, in the Euler-Maclaurin summation formula, and in Kummer’s half-proof of Fermat’s Last Theorem, for starters. One of my favorite theorems, Frank Adams’ computation of the image of the J homomorphism in the homotopy groups of spheres, uses the denominators of the Bernoulli numbers in its statement, apparently because they satisfy a certain divisibility criterion, though topologists to this day are looking for deeper reasons. The numerators, meanwhile, are more of a mystery, and it’s an open problem whether infinitely many primes $p$ divide the numerator of $B_{2p}$.

On the other hand, there’s a $p$-adic integral called the Volkenborn integral, which I learned about from Robert’s A Course in p-Adic Analysis. If $f$ is a continuous function on $\mathbb{Z}_p$, the Volkenborn integral is defined as a limit of Riemann sums where you sample at integer points: $$\int_{\mathbb{Z}_p} f(x)\,dx = \lim_{n \to \infty} \sum_{i=0}^{p^n - 1} \frac{f(i)}{p^n}. $$ Note that the factor of $1/p^n$ is the measure of the disk around $i$ of radius $|p^n|$, so that $\mathbb{Z}_p$ itself has measure 1; it’s a weird feature of $p$-adic analysis that these measures get larger as the disks get smaller.

There’s an “indefinite sum” operator $S$, defined on the natural numbers by $$Sf(n) = \sum_{i=0}^{n-1} f(i),$$ and extended to $\mathbb{Z}_p$ by continuity. We see that $$\int_{\mathbb{Z}_p} f(x)\,dx = \lim_{n \to \infty} \frac{Sf(p^n)}{p^n} = (Sf)’(0),$$ i.e., the integral is also a derivative.

Now the trick is to take the function $f(x) = (1 + t)^x$, where $t$ is some sufficiently small $p$-adic number, and write it two different ways. On the one hand, this function has an expansion in terms of binomial coefficients, $$(1 + t)^x = \sum_{k=0}^\infty t^k\binom{x}{k}.$$ This is obviously true if $x$ is a natural number, if we take $\binom{x}{k} = 0$ for $x < k$, and it’s true in general because the binomial coefficient functions are $p$-adically continuous. They’re also well-behaved for indefinite sum: $$S\binom{x}{k} = \binom{x}{k+1}.$$ It follows that $$\int (1 + t)^x\,dx = \frac{d}{dx}\left(\sum_{k=0}^\infty t^k\binom{x}{k+1}\right)\big\vert_{x=0}.$$ But $\binom{x}{k+1} = \frac{x}{k+1}\binom{x-1}{k}$, so its derivative at 0 is $$\frac{1}{k+1}\binom{-1}{k} = \frac{1}{k+1}\cdot\frac{(-1)(-2)\dotsm(-k)}{(k)(k-1)\dotsm (1)} = \frac{(-1)^k}{k+1}.$$ Therefore, $$\int (1+t)^x\,dx = \sum_{k=0}^\infty t^k \frac{(-1)^k}{k+1} = \frac{1}{t}\log(1+t).$$ You can take my word for it (I can talk about it separately, if people care) that this logarithm makes $p$-adic sense for small $t$.

Let’s put $s = \log(1+t)$. We’ve just proved that $$\int e^{sx}\,dx = \frac{s}{e^s - 1},$$ and the right-hand side is the function whose Taylor series gave us the Bernoulli numbers! Now, again taking my word for it, we can write $$e^{sx} = \sum_{k=0}^\infty \frac{s^k x^k}{k!},$$ and the convergence is nice enough that we can swap the sum and integral sign. We get $$\sum_{k=0}^\infty \frac{s^k}{k!} \int_{\mathbb{Z}_p} x^k\,dx = \sum_{k=0}^\infty B_k \frac{s^k}{k!},$$ or $$ \int_{\mathbb{Z}_p} x^k\,dx = B_k.$$

A number of nice properties of the Bernoulli numbers follow from this theorem plus some mild $p$-adic integration theory. For instance, the odd Bernoulli numbers vanish because for these $k$, $x^k$ is an odd function with zero first derivative. (The problem with $B_1$ is that the integral is really symmetric under the involution $x \mapsto -1-x$, and it’s not quite translation-invariant, so reflecting about 0 ends up introducing an error term of $-f’(0)/2$.) There’s also a nice bound on the size of the integral, $|(Sf)’(0)|$, in terms of the coefficients of the polynomial $Sf$, which says in this case that $pB_k \in \mathbb{Z}_p$. This means that the denominators of the Bernoulli numbers are squarefree -- probably not obvious from the definition! The full Clausen-von Staudt theorem -- that the primes dividing the denominator of $B_k$ (for $k$ even) are just those $p$ such that $p-1$ divides $k$ -- isn’t much harder.

Of course, the most amazing part of this theorem is that we can define these rational numbers with a $p$-adic integral that just happens to not depend on $p$. The first thing I did when I read this was to look for an analogous description in terms of an archimedean integral. Using Cauchy’s residue theorem, you can calculate Bernoulli numbers as contour integrals: $$ \frac{2\pi i B_k}{k!} = \oint_{|z| = 1} \frac{z}{e^z - 1} \frac{1}{z^{k+1}}\,dz.$$ I don’t think this is a great parallel to the $p$-adic formula, and it’s not quite as shocking, either, seeing as you could do the same thing for any function that’s analytic in a neighborhood of 0. However, I’m tempted by the fact that both the residue theorem and the Volkenborn integral show a certain unity between differentiation and integration...

Test Bank For Calculus: Early Transcendentals Single Variable, 12th Edition by Howard Anton

TABLE OF CONTENTS   PREFACE vii   SUPPLEMENTS ix   ACKNOWLEDGMENTS xi   THE ROOTS OF CALCULUS xv   1 Limits and Continuity 1   1.1 Limits (An Intuitive Approach) 1   1.2 Computing Limits 13   1.3 Limits at Infinity; End Behavior of a Function 21   1.4 Limits (Discussed More Rigorously) 30   1.5 Continuity 39   1.6 Continuity of Trigonometric Functions 50   1.7 Inverse Trigonometric Functions 55   1.8 Exponential and Logarithmic Functions 62   2 The Derivative 77   2.1 Tangent Lines and Rates of Change 77   2.2 The Derivative Function 87   2.3 Introduction to Techniques of Differentiation 98   2.4 The Product and Quotient Rules 105   2.5 Derivatives of Trigonometric Functions 110   2.6 The Chain Rule 114   3 Topics in Differentiation 124   3.1 Implicit Differentiation 124   3.2 Derivatives of Logarithmic Functions 131   3.3 Derivatives of Exponential and Inverse Trigonometric Functions 136   3.4 Related Rates 142   3.5 Local Linear Approximation; Differentials 149   3.6 L'Hôpital's Rule; Indeterminate Forms 157   4 The Derivative in Graphing and Applications 169   4.1 Analysis of Functions I: Increase, Decrease, and Concavity 169   4.2 Analysis of Functions II: Relative Extrema; Graphing Polynomials 180   4.3 Analysis of Functions III: Rational Functions, Cusps, and Vertical Tangents 189   4.4 Absolute Maxima and Minima 200   4.5 Applied Maximum and Minimum Problems 208   4.6 Rectilinear Motion 222   4.7 Newton's Method 230   4.8 Rolle's Theorem; Mean-Value Theorem 235   5 Integration 249   5.1 An Overview of the Area Problem 249   5.2 The Indefinite Integral 254   5.3 Integration by Substitution 264   5.4 The Definition of Area as a Limit; Sigma Notation 271   5.5 The Definite Integral 281   5.6 The Fundamental Theorem of Calculus 290   5.7 Rectilinear Motion Revisited Using Integration 302   5.8 Average Value of a Function and Its Applications 310   5.9 Evaluating Definite Integrals by Substitution 315   5.10 Logarithmic and Other Functions Defined by Integrals 320   6 Applications of the Definite Integral in Geometry, Science, and Engineering 336   6.1 Area Between Two Curves 336   6.2 Volumes by Slicing; Disks and Washers 344   6.3 Volumes by Cylindrical Shells 354   6.4 Length of a Plane Curve 360   6.5 Area of a Surface of Revolution 365   6.6 Work 370   6.7 Moments, Centers of Gravity, and Centroids 378   6.8 Fluid Pressure and Force 387   6.9 Hyperbolic Functions and Hanging Cables 392   7 Principles of Integral Evaluation 406   7.1 An Overview of Integration Methods 406   7.2 Integration by Parts 409   7.3 Integrating Trigonometric Functions 417   7.4 Trigonometric Substitutions 424   7.5 Integrating Rational Functions by Partial Fractions 430   7.6 Using Computer Algebra Systems and Tables of Integrals 437   7.7 Numerical Integration; Simpson's Rule 446   7.8 Improper Integrals 458   8 Mathematical Modeling with Differential Equations 471   8.1 Modeling with Differential Equations 471   8.2 Separation of Variables 477   8.3 Slope Fields; Euler's Method 488   8.4 First-Order Differential Equations and Applications 494   9 Infinite Series 504   9.1 Sequences 504   9.2 Monotone Sequences 513   9.3 Infinite Series 520   9.4 Convergence Tests 528   9.5 The Comparison, Ratio, and Root Tests 534   9.6 Alternating Series; Absolute and Conditional Convergence 540   9.7 Maclaurin and Taylor Polynomials 549   9.8 Maclaurin and Taylor Series; Power Series 559   9.9 Convergence of Taylor Series 567   9.10 Differentiating and Integrating Power Series; Modeling with Taylor Series 575   10 Parametric and Polar Curves; Conic Sections 588   10.1 Parametric Equations; Tangent Lines and Arc Length for Parametric Curves 588   10.2 Polar Coordinates 600   10.3 Tangent Lines, Arc Length, and Area for Polar Curves 613   10.4 Conic Sections 622   10.5 Rotation of Axes; Second-Degree Equations 639   10.6 Conic Sections in Polar Coordinates 644   A Appendices   A Trigonometry Review (Summary) App-1   B Functions (Summary) App-8   C New Functions From Old (Summary) App-11   D Families of Functions (Summary) App-16   E Inverse Functions (Summary) App-23   READY REFERENCE RR-1   ANSWERS TO ODD-NUMBERED EXERCISES Ans-1   INDEX Ind-1   Web Appendices (online only)   Available in WileyPLUS   A Trigonometry Review   B Functions   C New Functions From Old   D Families of Functions   E Inverse Functions   F Real Numbers, Intervals, and Inequalities   G Absolute Value   H Coordinate Planes, Lines, and Linear Functions   I Distance, Circles, and Quadratic Equations   J Solving Polynomial Equations   K Graphing Functions Using Calculators and Computer Algebra Systems   L Selected Proofs   M Early Parametric Equations Option   N Mathematical Models   O The Discriminant   P Second-Order Linear Homogeneous Differential Equations   Chapter Web Projects: Expanding the Calculus Horizon (online only)   Available in WileyPLUS   Robotics -- Chapter 2   Railroad Design -- Chapter 7   Iteration and Dynamical Systems -- Chapter 9   Comet Collision -- Chapter 10         Read the full article