I ask because what I was specifically referring to was the feeling of making it past the intro level “real math” classes and slowly starting to realize that the focus for most of the professors/researchers were actually problems I could understand from a pretty basic level. (I went to a college that had no graduate program in pure maths.)

I had the idea that anything worth researching in math must require years of study to even be able to begin to understand. Are there problems like that? Absolutely. Are there interesting problems that are related that you can work on along the way that will help firther your understanfing? Absolutely.

The most important thing I have learned in math is consistently showing up with the attitude of just wanting to know more about mathematics. Sometimes that’s stuff someone else already found out about; sometimes it’s stuff you gotta find out about for yourself.

Hello, I just read your bad luck post and you seem to be just a bit further a long than I currently am down the math academia rabbit hole. In your post you mentioned that you had no idea what maths research was even? That's essentially my current knowledge on that topic. Do you have a better idea or any idea now? Thank you.

Hi! Where are you right now in school?

Hello, I just read your bad luck post and you seem to be just a bit further a long than I currently am down the math academia rabbit hole. In your post you mentioned that you had no idea what maths research was even? That's essentially my current knowledge on that topic. Do you have a better idea or any idea now? Thank you.

Hi! Where are you right now in school?

I’ve moved to @on-purpose-math-blog in case you are interested in following my most recent exploits.

A More Intuitive Topology

Topology is defined a bit oddly. Mostly,we know what sort of properties we want a “space” to have, but formalizing them to be defined using set theory is a little trickier.

The mixed metaphor I will use will be maps and lenses. It won’t be perfect, since it’s hard have a good intuition for “infinitely many.” Also, many intuitions generalize from very nice topologies called “manifolds,” and so won’t generalize perfectly.

What we really want to do with space is figure out what is close together, what an individual area looks like, but we don’t want to see individual points.

So, a topology should contain sets of points, and think of those as the areas we want.

Now, it can’t just be any collection of sets, so let’s think of some constraints we can impose on them.

1) If you can see two different areas, then you should be able to see what happens when you put both together.

In set theoretic terms, this means we want it to be closed under union.

There is no reason for it to just be a finite number. If we get infinite areas, when you put them all together, there is no reason for them to not also be like a space.

In fact, infinities let us make different shapes that we also want to be able to use.

So, it should be closed under arbitrary (both finite and infinite) union.

2) If you see two different areas, then you should also be able to only see areas where both are. You could think of putting the two filtering lenses on top of each other, or drawing only where the maps agree.

In set theory terms, we want it to be closed under intersection.

Unlike union, we don’t want it to allow all infinities. Think of if you have circles getting smaller and smaller.

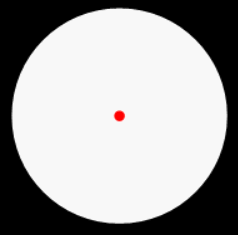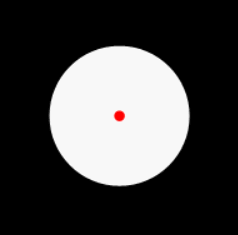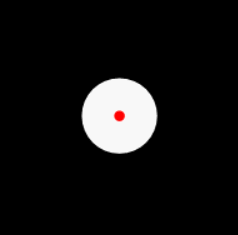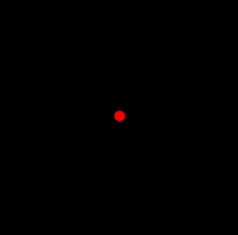
Then, if you could see the point they all share as an “area,” then we can see any individual point too. This is ok for some topologies, but we don’t want it to be a condition for all topologies.

That is, it should be closed under finite unions (but not necessarily infinite ones).

Note that this makes an asymmetry between the operations, which is fun and interesting.

3) It must contain both the empty set and the entire space.

If we want to see areas that aren’t near each other, for completeness, their intersection is the empty set.

If we take all of what we define as areas, they should cover the whole space, because we don’t want to focus on anything we can’t see.

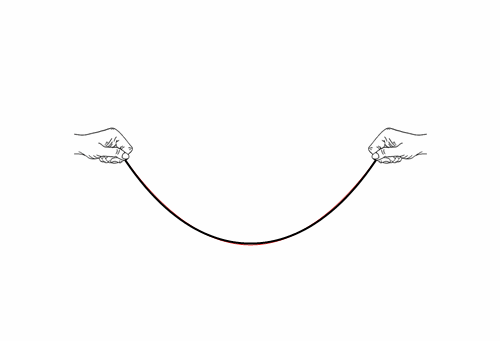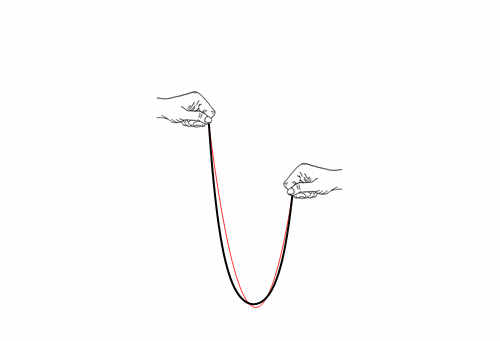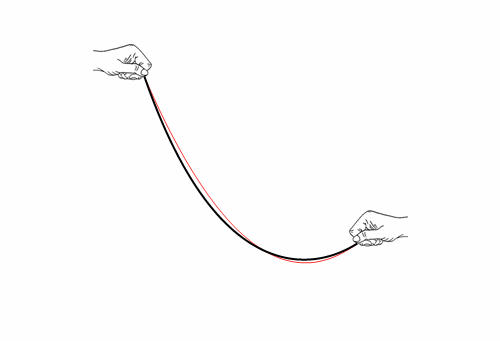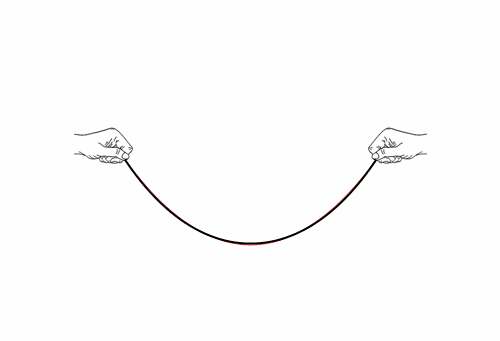
A rope is supported at its ends. What shape do you think it assumes? Galileo though parabola, in red. Wrong! Let’s cut Galileo some slack though. The right answer, so called catenary, is very close.

This is great :) My favorite is proof by ghost reference, what is yours?

Update on Summer School

Getting personal stuff out of the way first, I must admit that I wasn’t fully there today, as I have been having several... distressing yet illuminating conversations with my boyfriend about non-math stuff. I felt (weirdly) guilty about it, because I am getting distracted! That’s bad! But also we were focusing on the topics covered by Gabor Szekelyhidi, which are much more complex-analysis focused than I can easily keep up with anymore. I managed to swallow my pride and asked for a bunch of help on the problems and got the courage to ask some pretty basic questions. This leads me in to the math side of things.

Today I learned about the residue theorem, the indentation lemma, and thought a little bit more about the open mapping theorem. I also asked what a 1-form is, and got an explanation that made it seem as though it was something I should already be familiar with. I will write posts trying to explain each. These are as much for my benefit as anyone elses, so please comment/ask questions!!

Emily Does Summer School (also some stuff about Riemannian surfaces)

So, considering that I knew nothing about Kahler Geometry before starting this program (or algebraic geometry) I think things are going pretty well!! I have been following the lectures pretty closely (except algebraic geometry.. that will definitely take further study later). I got a pretty hard look at Truth today because I was completely lost during the algebraic geometry (ag) lecture and then tried to tackle the problem set to see if I could figure stuff out... and was not successful at all. Fortunately the TAs and professors who were with us helped me out, but I needed a lot of help and I can’t do math with an audience unless I am really comfortable/confident. Which... I wasn’t. Tomorrow should be better though. I am doing well at talking to students; everyone is very nice and, guess what, math people in general are not super outgoing and so I am fitting in very well socially. It is interesting to talk to the other students and learn about their schools, there are some students from really good math programs here! After today I should be better about talking to (not being scared by) the professors.

tl;dr, things are going better than expected!!

On to the math! According to the wikipedia page, a Kahler manifold is one with three compatible structures: (1) a complex structure, (2) a Riemannian structure, and (3) a symplectic structure. We skipped talking about (1) because most people should be pretty familiar with that by now (lol I haven’t taken complex analysis but w/e I’m managing). We also aren’t going to talk about (3) because apparently it is a fairly new branch of research and isn’t as accessible as (2).

SO! What is a Riemannian surface? We are working with Gabor Szekelyhidi slowly toward this concept from an analysis perspective; so far, (from what I can tell), a Riemannian surface is one you can create by stitching together copies of $\IC$ and adding points at infinity to create a compact manifold. You can then map this back to the complex numbers using holomorphic fuctions, and the identifications constructed through these functions allows you to do calculus on this manifold where you can circumvent certain problems, such as not having an injective square root function in the complex numbers (this part I am still unclear, so apologies if I made a mistake), as opposed to sitting and crying (idk, if you’re me you might do this anyway). The professor lecturing on analysis is explaining mainly through pictures, and I am hoping to be able to post something later with more detailed notes. 

We are working much faster toward this concept from an algebraic perspective, because the dude teaching ag, Claudiu Raicu, an associate professor at Notre Dame, is really whipping us along. This is an interesting way to go about doing things, because as far as I know, only a few students have enough of a background in ag to keep up, or even have really any idea what is going on. According to ag, a Riemann surface is a non-singular (affine or projective) curve over the field of complex numbers. A Riemann surface is compact if and only if it is projective. 

There are a *lot* of concepts to unpack here, and each is pretty heavy. A lot of what we are doing involves quotienting the ring of polynomials in 2 or 3 variables by polynomials and determining the size of the result to give you information about the multiplicities of intersections of the polynomials. It’s nice that I am using my algebraic knowledge (oh man, am I digging out ideas that I honestly thought I wouldn’t use again. Turns out local rings are *super* important, and sou is Bezout’s Theorem), and I will need to dredge through this very carefully this week and in the future to make sure I am understanding everything.

The final lecturer is Andrei Jorza, who is lecturing on applications of Riemannian surfaces to number theory. We constructed a fundamental domain for the upper half plane in the complex numbers, and are using the properties of arithmetic on that domain to help prove an equivalence discovered by Ramanujan... That I am not going to get in to right now. To be honest I have been paying the least amount of attention to these problems because they appear to be straight forward; showing that summations are equivalent, and etc. They are definitely good practice and I will do my best to type up those notes and problems later as well.

I will try to update when I can!

It’s kinda sad how children automatically label themselves as “dumb” when they can’t do or understand MATH… Seeing how the world puts so much emphasis on MATH, nobody gets credit when they’re amazing at writing, or music, or ART… Because the only thing that really matters is the fucking quadratic formula, right?

Ancient Greek, geometric view of prime numbers.

More Travel

Off to the Notre Dame Summer School in Kahler Geometry today!! I am quite nervous, and will have to really go out of my way to talk to people and make friends, as opposed to what I normally do, which is to avoid eye contact with everyone and pretend I’m the only person who exists while eating alone. I am expecting to be quite exhausted. I am also breaking out one of my spiral-bound blank-paper notebooks one of my friends gave me for graduation!

One of the consequences of committing to math is that I am now doing a *lot* of flying. Unfortunately I’m not old enough to get drunk at the airports quite yet. Oh well, at least I can absorb myself in the math books I have. Coming with me on the flight in my carry on is Pinter’s Abstract Algebra (for practice and solidification of concepts), Munkres’ Topology (because obviously), and one of the complex analysis books I got in order to start upon that subject.

I might do a daily post or something to help document the math we are going over and blow off steam, if I need to.

Hello! A friend asked 'what's your profile picture is about?'

Hi there,

The image is a visualization of a pathological object in topology, called Alexander’s horned sphere. This object has some counter-intuitive properties: its interior is simply connected (you can shrink any loop to a single point), but the exterior is not (there are loops “around the horns” that cannot be shrunk, such as the red one drawn on the picture), implying that the Jordan-Schönflies theorem doesn’t hold in three or more dimensions.

Though the notions are intuitively quite accessible, I cannot blame you if this sounds too advanced, in which case I merely present you the horned sphere as a cool fingery fractal. Notice how the fingers keep on intertwining but never knot together or self-intersect.

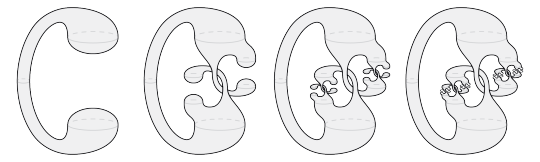
Thanks for asking!

I’m still slowly working through the calculus outlines. I think the best way to manage myself so I don’t get discouraged is to adjust my expectations, as in “Yes! It’s okay if you take your time to relearn this stuff from 4 years ago, even if it means you only get two sections done today!” I’m going to review the trig identities also. I just worked through that chapter and they included all of them in much greater detail than I have ever seen.

Also, I am done editing the papers on my end!! Now I just have to wait to hear back from my newly-married advisor on his thoughts...

There is a particular kind of open-ended idea which I call the blue-sky idea. Namely, someone sitting at his desk with his feet up and looking out the window has come up with some concept, and now hopes that he or someone he knows can come up with a good way of using that idea. At conferences one sometimes encounters mathematicians who specialize in this sort of idea, button-holing everyone who can’t manage to avoid them and inflicting their most recent blue-sky idea on them. … When one looks at the history of mathematics, it may seem that a lot of the most important developments have come out of blue-sky ideas. But in fact, from what I know, this is almost never the case. Good ideas always arise out of some existing line of thought, and it is only after when has put a lot of effort in that one realizes that there is some gradiose general concept that underlies all one’s work. For instance, I am pretty sure that Eilenberg and Steenrod didn’t sit down together over a beer one day and say, “Wouldn’t it be neat to draw up a set of axioms for a thing called a category and then invent a concept called a functor, and then see if these would be useful for anything?” It’s pretty clear that in fact they noticed that in algebraic topology the same sorts of situations keep coming up over and over again, and one keeps seeing different theorems with different subject matter, where somehow the proofs always turned out to be more or less the same. So they saw (I believe) the need for a vocabulary and a conceptual framework that would enable mathematicians to talk about all this in a unified way. Ergo: category theory.

Lee Lady, How to do mathematical research (via isomorphismes)

I really hate the “anyone can learn X” rhetoric, even though I am myself guilty of spreading it among my students. 

Could I, theoretically, learn, say, molecular biology in a year? no, let’s take something even close, like arithmetic geometry? Sure. Given if I had time available, if I had US citizenship and enough savings so I didn’t have to work and could dedicate myself to studies, if I could constantly talk to the people in the field and ask them endless questions, if I was motivated, if people in my life supported me in this decision, if I had a dream to have a job in that field…

But I am in grad school and teaching, and I can’t make the time to study a new subject. This is shaping who I am. I am not a permanent resident of the country where I live, and that is shaping the way I see the world, and so also who I am. I, Alex, am not the kind of person who has thousands of dollars saved for a day when I want to pursue a different subject – I like to wear good clothes and eat good food and travel instead. That is who I am. I have extreme social anxiety and I can’t talk to people, especially people I need something from (like answer to my question). That is who I am. I was various degrees of depressed most of my life, I don’t have the energy or motivation required to learn a subject, no matter how much it interest me. That is also who I am right now, even if it’s a bad thing. My family and friends offer the emotional support of a coffee table. This is also making me who I am. I always consider all possible outcomes and make sure I cover all mys bases, in case something doesn’t work out, so I don’t have a single dream occupation, “all or nothing”…

So who is that person who can sit down and learn arithmetic geometry in a year? It’s not me. I would have to become someone different – and that’s a good thing! – but it would be this new person who is able to do it.

Starting slow

I am having to adjust my expectations quite a bit. I am not able to read more than a section a day right now (problems included). This is not for lack of time but more for mental reasons. I just got back from a lot of traveling/hiking around, and only now am in a place where I don’t have things I need to do for other people. I am finally trying to address things like my eating, reading, and sleeping habits, which kind of went to shit during the semester. I found it difficult to maintain any kind of schedule during college, and am looking forward to fixing this.

In the mean time, I am having to accept slightly less productivity on my three current projects (I know, I know). The one that I am choosing to give priority at present is working through calculus outlines - starting at the *very* beginning. The work can be particularly tedious, but I definitely need practice with bookkeeping and dealing with “simpler” equations.

I hope to finish section 18 today. I can’t believe the number of times I have written that, but I believe it is possible now and I will continue to try.