hippasos - Tumblr blog

hippasos · 8 years

Text

Fibonacci prime

The Fibonacci sequence is one of the most fascinating patterns in nature. You can easily calculate the n-th fibonacci number F(n) by adding the n-1-st and n-2-nd Fibonacci number, e.g. you begin with 0 + 1 = 1, 1 + 1 = 2 = F(3), then 1 + 2 = 3 = F(4), 2 + 3 = 5 = F(5), 3 + 5 = 8 = F(6), and so on. You get the sequence

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

But one mindblowing fact is, that you can sum up this infinit sequence by just one number 89.

If you look at

0.0 0.01 0.001 0.0002 0.00003 0.000005 0.0000008 0.00000013 0.000000021 0.0000000034 0.00000000055 ... +___________________ 0.01123595505618... = 1/89

and add them, you get 1/89.

89 is a Fibonacci number (see sequence above) and something which we call Fibonacci prime. This is a Fibonacci number which is also a prime number. It is an unsolved mathematical problem, if there exist infinitely many Fibonacci primes. Solve it and become famous! ;-)

The really mindblowing fact seen above is, that we can write

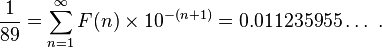
where F(n) is the n-th Fibonacci number. This means, if you take each Fibonacci number F(n), divide it by 10 raised to the power of its position in the Fibonacci sequence plus 1 and add them all together, you get 0.011235955…, which is just 1/89.

This is, why I like 89. :)

If you want to know more about it and what general pattern underlies this strange number, I recommend you to visit

http://www.mathpages.com/home/kmath108.htm

Have a nice week!

tl;dr: 89 is a nice number. The digits of 1/89 form the Fibonacci sequence by addition and multiplication with 10 raised to minus the power of its position in the Fibonacci sequence plus 1.

Sources:

https://en.wikipedia.org/wiki/89_%28number%29

https://en.wikipedia.org/wiki/Fibonacci_prime

https://en.wikipedia.org/wiki/Fibonacci_number

#fibonacci #prime numbers #89 #number theory

5 notes · View notes

hippasos · 8 years

Photo

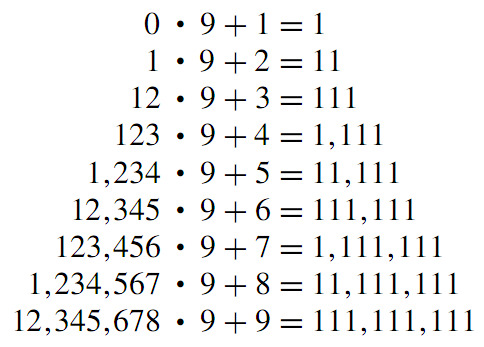
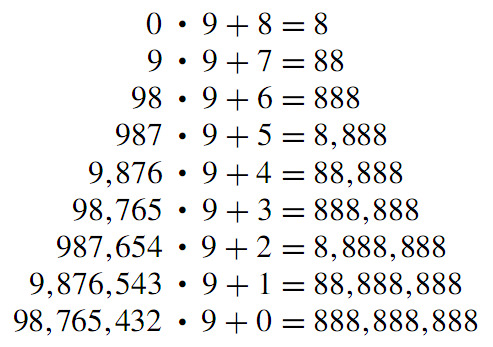
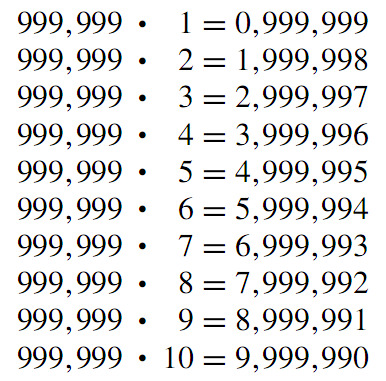
Amazing pattern of numbers. - Source: http://mathandmultimedia.com

#numbers #algebra #pattern #math

5 notes · View notes

hippasos · 8 years

Text

Proof: Euclidean Algorithm

One of my favourite proofs to show the theorem of the extended Euclidean algorithm using ideals (ring theory):

Let a and b be elements of Z. Then there exist x,y in Z, s.t.

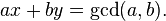
Proof:

gcd(a,b) ϵ (gcd(a,b)) = (a) + (b) = {ax + by | x,y in Z}. Q.E.D.

PS: The ( . ) is the notation for the ideal generated by a set.

#algebra #ring theory #euclidean algorithm #proof

0 notes

hippasos · 8 years

Photo

Mathematics writes the saddest stories. ;-)

#geometry #parallel lines #funny

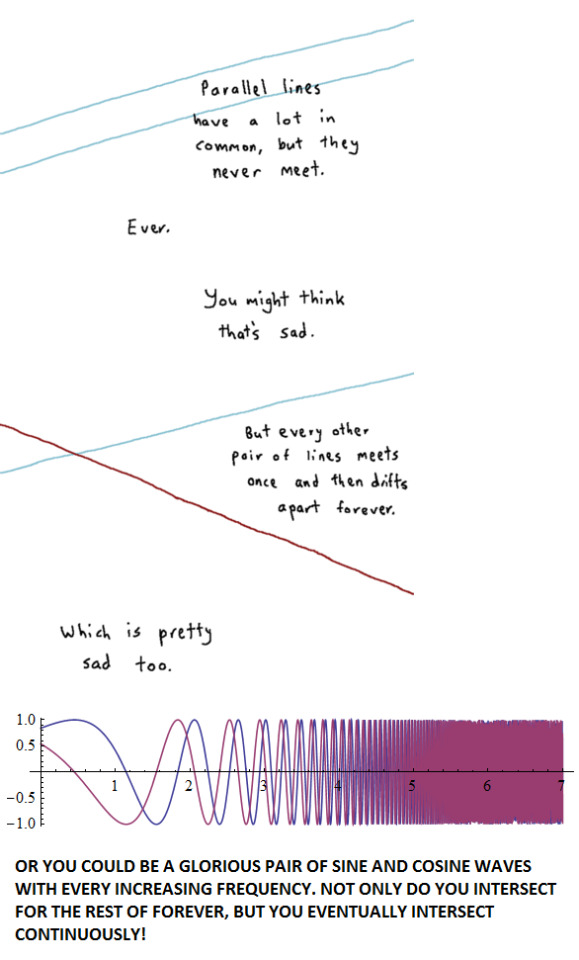
267 notes · View notes

hippasos · 8 years

Photo

1. Copy sqrt(cos(x))*cos(300x)+sqrt(abs(x))-0.7)*(4-x*x)^0.01, sqrt(6-x^2), -sqrt(6-x^2) from -4.5 to 4.5

2. Insert it in the Google Search.

3. Send it to your loved one. ;-)

#love #math #analysis #graph

0 notes

hippasos · 8 years

Text

Continuation: discrete differential & integral calculus

Here is the continuatiuon you hopefully longed for. ;-)

But in this post we will get to know some formal stuff. I hope it won’t be too boring. ;-)

At the end we will be able to calculate some “closed” formulas.

Last time we saw the Gaussian sum-formula and another Faulhaber-formula of the form

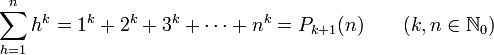
We wanted to construct a tool which gives us a standard procedure to get such formulas. We can construct it by discrete analogons to 1.) the derivative of a function and 2.) the integral or antiderivate. I recall our notations:

sum_{i = 1}^{n} i := 1 + 2 + ... + n for the sum from i = 1 to n and int_{x}^{y} for the integral in the interval [x,y].

Let's start. :-)

Definition (disrete derivative): (Δ f)(x) = f(x+1) - f(x) is called discrete derivative of the function f: Z --> R. Δ is the so-called difference-operator.

This is a disrete analogon to the derivative df/dx = lim_{h->0} (f(x + h) - f(x))/h. For the falling factorial (x)_{m} defined as

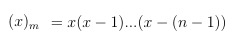
we have the same derivative rules we know from school (cf. http://mathworld.wolfram.com/FallingFactorial.html):

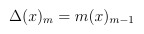
(take a paper and calculate it with the definition above!),

Nevertheless here is a short proof:

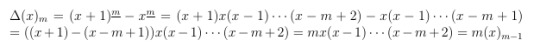
In addition the binomial coefficient "x over k", notated (x // k) := (x)_k/k!,

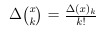
has the discrete derivative Δ(x // k) = (x // k-1).

We can define 2^x as

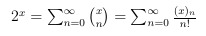
which is a real analogon to the series of

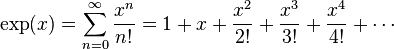
d/dx exp(x) = exp(x), analoguely Δ2^x = 2^x.

We can also define a discrete antiderivative. Let f: Z --> R, then F is called discrete antiderivative, if ΔF = f. This is the same pattern a continuous antiderivative is defined (F' = f) and we write

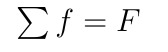
Obviously we have the following sum rule:

which is just a matter of calculating a telescoping series. But this is a discrete analogon to the fundamental theorem of calculus!

With the translation

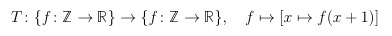
we can write Δ = T - id and get the following rules, which should be well-known in a slightly other form from analysis. ;-)

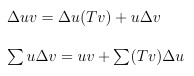
The last rules for

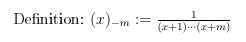
are given without proof (the proof is just a matter of calculating things):

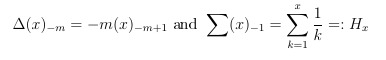
Now we have the basis for calculations with the so-called formal power series.

Maybe in one of my future posts, I will explain what these cruel “series” are and which rules of calculation exist for this type of “series”. Then we would be able to calculate closed formulas for a lot of other cases, e.g. the Fibonacci sequence.

But up to now we can calculate “easy” formulas! ^^

Here is an example how to calculate a formula with our tools:

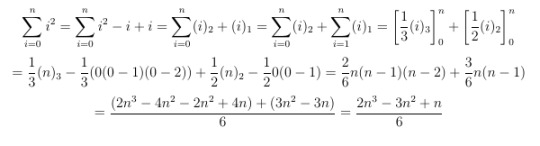
Now we have a closed formula for the sum sum_{i=0}^n i^2, which is correct, if we confer Faulhaber’s formula (cf. https://en.wikipedia.org/wiki/Faulhaber's_formula). We have reached our goal!

PS: For those, who want to calculate the discrete derivative of something or who wants to calculate a closed formula, here are some problems: f(n) = (-1)^n · x, g(n) = |n|, sum_{k=1}^n k^4. Have fun! :-)

tl;dr

We defined the discrete derivative (Δ f)(x) = f(x+1) - f(x) and antiderivative with ΔF = f. The falling factorial (x)_{m} = x (x-1) ... (x-(n-1)) gives us in most cases nearly the same rules as in analysis. We can now calculate easy formulas! :-)

#integral calculus #differential calculus #discrete mathematics

0 notes

hippasos · 8 years

Photo

Some nice topological theorems! :-)

I explained the one which results from the Bursuk-Ulam theorem and gave a short more intuitive than mathematically correct proof.

You can read it following especially the last hashtag: #borsuk-ulam #algebraic topology #covering spaces #mathexplainsworld

fyi: The promised part about the easy calculation of sum formulas by difference calculus will follow soon.

that moment when u open a topology book to some weird shit like this which your brain now registers as completely plausible and reasonable from all the damage your math major has done to your mind and for a fleeting, fleeting second of lucidity u wonder to urself “wtf am I doing with my life?”

#borsuk-ulam #algebraic topology #mathexplainsworld

2K notes · View notes

hippasos · 9 years

Photo

Carl Friedrich Gauß was a great German mathematician of the 18th/19th century who founded the non-Euclidian Geometry and explored many theorems of Number Theory, normal distribution and integral calculus. We can see him on the 10 Deutsche Mark banknote. Many people know the story of the little Gauß. When Gauß was 9 years old his teatcher Büttner gave his pupils the task to calculate the sum of the numbers from 1 to 100. Gauß surprised his teacher by solving the problem in a very short time. He formed 50 pairs of the sum 101 (1 + 100, 2 + 99, 3 + 98,...) and got 5050 as a solution. With the words "Ligget se" (Low German: "Here it is") he put the paper on the teacher's desk.

This pattern of adding numbers is the same as in the Gaussian sum-formula

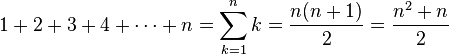
Normally you get this formula first by intuition, i.e. you add a few numbers and look at it carefully to get the general idea of the formula. Then you prove it by induction. We will see, how to solve such a formula by induction.

(Experts might skip the following proof. ;-))

Proof: First we have the beginning of induction. We show that the formula is true for one n in the natural numbers. When we are done, we will show that the formula is true for any n by proving that the formula is true for n+1. In this case (n+1), we assume that the formula is true for one n in the natural numbers. But if we have shown that the formula is true for one n in the naturals and for any n+1, then we can see the following. If it is true for n = 1, then it's also true for n = 1 + 1 = 2. But then it is true for n = 2 + 1 = 3, but then also for n = 3 + 1 = 4 and so on...

So we will have shown that the formula is true in general. That's the idea behind it. This is enough explanation, let's start the proof. ^^

Begining of Induction for n = 1: We just fill in n = 1:

(1*(1 + 1))/2 = (1*2)/2 = 2/2 = 1.

The formula is correct. :)

Induction step: We assume the formula is correct for one n in the natural numbers and prove the formula for n + 1, i.e.

((n+1) * (n + 1 + 1))/2 = ((n + 1)*(n + 2))/2 = (n² + 3n + 2)/2 = (n² + n)/2 + (2n + 2)/2 = (n² + n)/2 + (n + 1)

Now we can use our assumption: 1 + ... + n = (n² + n)/2.

(n² + n)/2 + (n + 1) = 1 + ... + n + (n + 1).

So we have: 1 + ... + n + (n + 1) = ((n+1) * ((n + 1) + 1))/2 and this is the formula for n + 1. Q.E.D.

I think some people, who had mathematics in school, know this proof by induction. But next time I will describe an other way of proving this with a machinery of discrete differential and integral calculus.

We will construct an analogon to d/dx, the derivative of a function, and one to the integral.

I will use the following notation:

sum_{i = 1}^{n} i := 1 + 2 + ... + n for the sum from i = 1 to n and int_{x}^{y} for the integral in the interval [x,y].

It would be mean to stop here without giving you an intuition how the analoga look like. ;-)

Maybe you have already seen this, but we know that

sum_{i = 1}^{n} i = (n² + n)/2 = n²/2 + n/2.

If we look at the first summand n²/2 it reminds us of the usual antiderivate of f(x) = x, which is F(x) = x²/2 (Remark: because F'(x) = f(x)).

Let's look at sum_{i = 1}^{n} i² = 1 + 4 + 9 + 16 + ... + n². The formula is given by

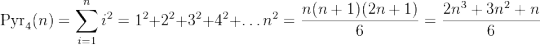
(square pyramidal number)

It reminds us of the antiderivate of f(x) = x², which is F(x) = x³/3.

This shows that the sum has something to do with the integral and we will make this "has something to do with" more precise next time.

But if the sum is somthing like the integral, what's the analogon to the derivative of a function? O.o

That's a great question, but we will see, how we construct a discrete analogon to the derivative

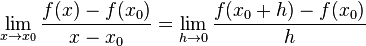
Why should we construct these tools?

With these tools we will, find a formula for any sum which look like the two above (cf. e.g. Faulhaber's formula). Well, we can proof the formula for sums with induction (this could be an exercise for the second formula), but we always must have an idea of the general formula. With the tool we construct, we won't have to be creative. ;-)

This is a great advantage! See you then!

tl;dr

The Gaussian sum formula is given by

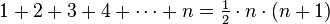
and can be used for the short addition of the natural numbers from 1 to 100. The proof is just induction. We can find discrete analogons to the derivate and the integral of a function in differential and integral calculus. The analogon of the integral is the sum. Next time we will construct an analogon to the derivate. These analogons will help us to find very easily “closed” formulas for diverse sums.

#integral calculus #differential calculus #discrete mathematics #gauß

9 notes · View notes

hippasos · 9 years

Photo

This is a mathematical Sudoku based on the Sudoku in Karpfinger’s and Meyenberg’s textbook “Algebra” (2013, p.9) which is a really good understandable book about Abstract Algebra. :-)

For solving this Sudoku you have to apply the rules of Sudoku (in the 3x3-boxes you should only fill in either x,y,z or a,b,c; there should not be any repetition of elements in vertical or horizontal lines) and you have to assume that G={a,b,c,x,y,z} is a group with the operation G x G --> G above.

Have fun! ^^

PS: Here is a short repitition. What is a group?

That’s just a set of elements G with an operation *:G x G --> G, s.t.

1.) For every g,h,i in G: (g*h)*i = g*(h*i)

2.) There exists a(n unique) neutral element e in G, s.t. e*g = g = g*e for every g in G.

3.) For every g in G there exists an (unique) inverse g^(-1), s.t. g*g^(-1) = e = g^(-1)*g

A typical example of a group are the integers ..., -3, -2, -1, 0, 1, 2, 3, ... with the standard addition +. The neutral element is 0 and the invers to x is -x.

Christian Karpfinger and Kurt Meyberg. Algebra. Springer Spektrum Verlag, Heidelberg, 3rd edition, 2013.

#abstract-algebra #group #sudoku

9 notes · View notes

hippasos · 9 years

Text

Shape of the universe

I think the universe is pure geometry - basically, a beautiful shape twisting around and dancing over space-time. - Antony Garrett Lisi

Last time we discussed the shape of the universe as a Torus. There could be another type of shape: the 3-Sphere. How can we imagine such a shape? Well, it's just like the 3-Torus, our mathematical object is 4-dimensional. To get some intuition, we will start with lower dimensions.

We imagine a 1-Sphere, i.e. just a circle. We call it S^1. This is the 1-dimensional universe of a 1-dimensional creature which might be a dot. Our one dimensional friend is called "Karl" (obviously Karl is a German guy).

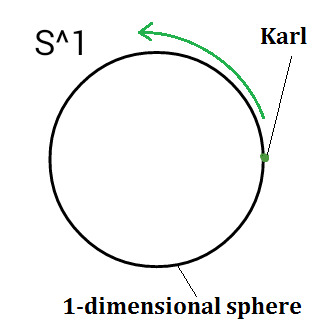
If he moves around in his 1-dimensional universe, he can just go forward or backwards. If he goes in the direction of the green arrows, he will get back, where he started. This phenomenon will also occur in higher dimensions.

Now we go one dimension higher. In the following step we will construct a 2-sphere. This construction will help us getting an intuition of the 3-sphere and construct a new universe for Karl who has grown into a 2-dimensional creature.

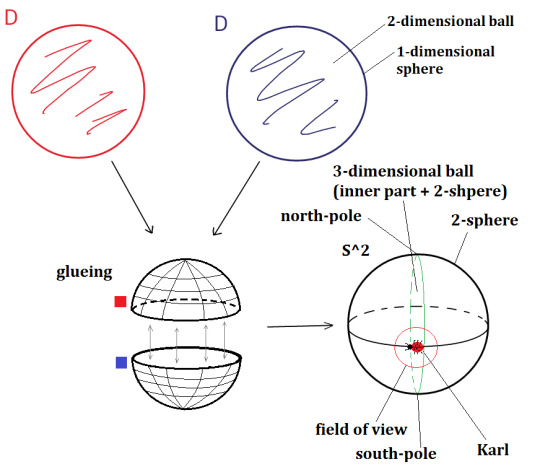
We take two copies of a disc (see picture). In the blue and the red disc D now the 1-dimensional sphere has become the boundary of a 2-dimensional ball. If we buckle the 2-dimensional balls to hemi-spheres and glue them at their boundaries, we get a 2-dimensional sphere. Now we look at Karl. He now goes along the green line (Greenwich) starting at the north pole, changing the hemi-sphere, going to the south pole, one more time changing the hemi-sphere and gets back, where he started, if he goes long enough straight forward. Recognize that the north and the south pole are the middle points of the previous 2-dimensional balls. Let's consider Karl's field of view. He only knows his 2-dimensional world and might think that he lives on a plane and not on the surface of something 3-dimensional, a 3-ball (this is, what we called locally Euclidian last time). Indeed this is the way mankind imagined for a long time the shape of the earth we are living on. Sailors even feared to fall down at the end of the earth, because they thought it was a plane.

Now we do the same one further dimension higher. This is an operation in the 4-th dimension, so we can't really imagine it. But we have to do the same. We just glue the boundaries of two 3-dimensional balls together. The boundaries are 2-Spheres. How to buckle the 3-dimensional balls is not imaginable, but we can call one ball the northern hemi-sphere and one the southern hemi-sphere, like before. The north-pole and south-pole is the middle point of the corresponding hemi-sphere, like in the 3-dimensional case.

Karl has grown into a 3-dimensional creature and learned to drive a rocket. He starts at the north pole of the northern hemi-sphere and goes up to a point at the "equator", i.e. the boundary of the northern hemi-sphere (1). In the southern hemi-sphere he goes to the south pole (2) and arrives at the next point of the "equator" (3). He changes the hemi-sphere and gets back, where he started (4). Like in the 2-dimensional case, he would also recognize his universe as something 3-dimensional, although the shape of the universe is 4-dimensional.*

Many scientists don't prefer this type of universe. They think the universe is flat, i.e. that the parallel axiom of Euclid holds, because the so called inflation-theory postulates it. But the parallel axiom doesn’t hold for a spherical universe, because two parallel lines going straight forward will intersect each other at some point. in such a universe. There are a lot of scientists who also prefer a infinite universe. But is this logical? Here are some questions, you have to wonder: How can such a universe grow infinite in a finite amount of time? Was it finite at the time of the Big Bang? How can an infinite universe expand?

I think this is the last post of our series #mathexplainsworld. There are a lot more topics about this theme, but I think next time I will start some interesting inner-mathematical topics and how mathematics influences parts of our everyday life. Be surprised! ;-)

Source: *Spektrum der Wissenschaft, Sept. 2004, pp. 90-91. More informations: http://www.avgoe.de/StarChild/DOCS/STARCH00/questions/question35.html Last questions: http://www.thenakedscientists.com/forum/index.php?topic=52438.0

Pictures: Made with Paint.

#mathexplainsworld #sphere #algebraic topology #topology #universe #shape of the universe

0 notes

hippasos · 9 years

Quote

So say you’re locked in a dark room, you’re two dimensional and trapped on the surface of a doughnut.

Rod Gover, describing topology (via mathprofessorquotes)

Let’s begin with a nice quote which describes the world of our 2-dimensional friend of the last post of our series #mathexplainsworld. (In this post I would like to add some information to my last post. It is not a new article of the series.) To get a feeling for the life of a 2-dimensional creature living on a 2-Torus, there are different games on the Torus: http://www.geometrygames.org/TorusGames/index.html.de (German) http://www.geometrygames.org/TorusGames/index.html.en (English) The website includes games such as: tic-tac-toe, mazes, crossword puzzles, word search puzzles, jigsaw puzzles, chess, pool, gomoku and apples. Although it is developed for children who are 10 years old, I think it gives an awesome possibility to train spatial sense. And games like chess are classic. ;-)

#mathexplainsworld #universe #torus #algebraic topology #topology #game

414 notes · View notes

hippasos · 9 years

Photo

"Space: the final frontier. These are the voyages of the starship Enterprise. Its continuing mission: to explore strange new worlds, to seek out new life and new civilizations, to boldly go where no one has gone before."

This is the intro of many episodes of Star Trek. But is the universe infinitely big or is it finite? This question is not really clarified. We will discuss two different topological structures of the universe, the first one in the following post.

Stephen Hawking to Homer: "Your theory of a doughnut shaped universe intrigues me. I may have to steal it." (The Simpsons, episode: "They Saved Lisa's Brain")

A finite space (better: compact topological space) could be a doughnut, in other words a torus. This is the word a mathematician prefers. In particular a doughnut is a 2-Torus. A 2-Torus T = S^1 x S^1 is described as the Cartesian product (this is the "x") of two 1-Spheres S^1, i.e. two circles. We can imagine forming the Cartesian product as the three dimensional figure which is created by going around the first circle with the second one. This is exactly the shape of a doughnut.

The universe is not exactly a doughnut, but it's the 4-dimensional analogon of it, a 3-Torus which is described as S^1 x S^1 x S^1. So it has some properties in common with the 2-Torus, but this comes later...

First we want to see why we should assume such a strange shape. And the answer is: It has something to do with the cosmic microwave background (CMB). There are several reasons to assume, that in the early time of our universe after the so called Big Bang, when it cooled down, protons and electrons reacted to hydrogen atoms which induced "de-coupling" of radiation and matter. So the universe was penetrable for radiation, because there was no scattering at electrons. By the growth of matter, in some parts of the agglomerated matter became more weighty and had a higher force of gravity. This led to a fluctuation of density in the early universe. But now photons had to face gravity in the more dense regions. This is the reason for fluctuation of temperature in the CMB. Normally the average spectrum of the microwave radiation is that of a black body, i.e. 2.725 Kalvin. But because of the reasons before, the radiation became the more colder the more dense the parts of the universe were. The following picture shows the fluctuation of temperature of the CMB:

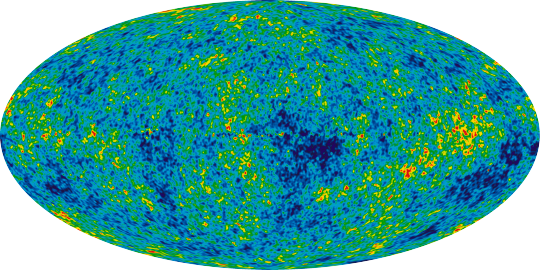
Frank Steiner and his team of the University of Ulm showed that the torus-universe is compatible with the CMB (for more information: Spektrum der Wissenschaft Jan. 2009, pp. 24-29).*

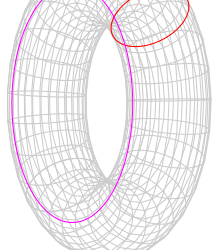
(Mathematically) reasonable implications of this result are the following. We look at our doughnut, the 2-Torus. If a little 2-dimensional creature would life on the surface of the torus and it would go straight in a forward direction, then it would get to the place, where it started. The reason is described in a simulation I posted some month before (#thefundamentalgroupofatorusisabelian). The simulation shows how to glue a paper, s.t. it forms a torus. In the following picture the opposite sites of the rectangle are colored green and purple.

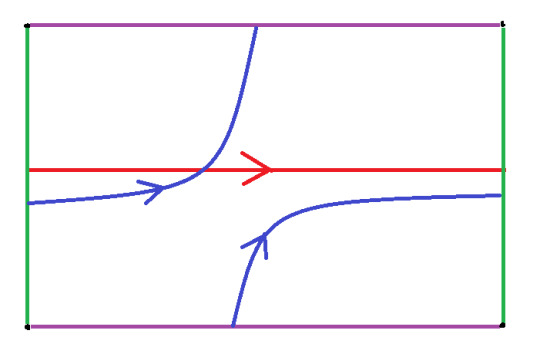
Our two-dimensional friend could go the red or the blue way to get back where it started. Furthermore our friend would think that his universe might be two dimensional (locally euclidan, in the sense, that it is homeomorphic to the IR^2). Analogously we think our universe is 3-dimensional, because we only have a local point of view. But in reality it could be 4-dimensional, like the 3-Torus. In addition: If our universe was a 3-Torus, we could go by a rocket in one direction and get back where we started! :)

Next time we will discuss the second interesting structure of the universe. See you then!

Source: *Spektrum der Wissenschaft Jan. 2009, pp. 24-29.

Pictures: https://upload.wikimedia.org/wikipedia/en/2/2d/ST_TOS_Cast.jpg http://i.dailymail.co.uk/i/pix/2015/03/02/263E2E5600000578-2975606-The_formula_written_on_Homer_s_blackboard_above_is_said_to_predi-a-14_1425299801754.jpg https://upload.wikimedia.org/wikipedia/commons/thumb/8/81/Torus_cycles.svg/220px-Torus_cycles.svg.png https://upload.wikimedia.org/wikipedia/commons/3/3c/Ilc_9yr_moll4096.png

#algebraic topology #torus #mathexplainsworld #universe #topology

1 note · View note

hippasos · 9 years

Photo

In George Orwell's distopian novel "Nineteen Eighty-Four" the author describes a world divided into three pieces by totalitarian or authoritarian states which are always fighting against each other. The people living in the state "Oceania" are under constant surveillance by televisions and have to worship the great "Big Brother" whose existence is not even clear. The protagonist tries to escape from the system to get privatcy, but in the end he becomes a part of the omnipresent system after a brain-washing and loves the "Big Brother". Well, that's a nice story, but why is it a part of the series "math explains world"? Last time we had the Borsuk-Ulam-theorem. It gives an awsome application in this context. :) Let's consider the map of Orwell's distopian world.

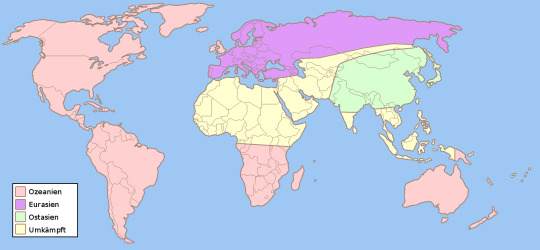
There are three countries: Oceania, Eurasia and Eastasia. Now we wounder, if there is a pair of antipodal points, s.t. one of the teritories of the countries includes this pair of points! Further more we wounder, if this is always the case. So is it possible, that there exists a pair of antipodal points, s.t. in any constellation of divisions of the world into three teritories this pair is included in one of the teritories?

The answer is YES!!! :D You can use any division into three pieces, but there is always a pair of antipodal points in one of the three teritories. OK, to be mathematically correct, the division of the 2-Sphere (notation: S^2), which is in our case just the surface of the earth, into three sets has to be, s.t. this sets are closed. This means: If we consider the boundaries of the sets, then their boundaries have to be in each set they're belonging to (see: https://en.wikipedia.org/wiki/Closed_set). Further more there have to be exactly three teritories (not 4 like in the picture). The lemma is the following:

Whenever S^2 is expressed as the union of three closed sets C1 , C2 and C3, then at least one of these sets must contain a pair of antipodal points {x,−x}.*

The question is: Why?

Proof: Let's consider S^2 as a subspace of the IR^3 and let d be the distance from one point of the 2-sphere to an other point on this sphere by going a path on the sphere. This is just the distance you know in real life. If you go from your home to an other city by car and you can drive just the linear distance, then you are not going the direct way, but a way which is determined by the curvature of the earth which we can approximate by a 2-sphere. We now define three distance functions, D_i: S^2 --> IR for i = 1,2,3 mapping a point x to the distance of this point to C_i, i.e. D_i(x) = inf_{y in C_i}(d(x,y)). What is this cruel map describing? The inf (read: Infimum) of something searches for the smallest value of d(x,y) by varying the point y in C_i. These D_i are continuous. Now consider the map f: S^2 --> IR^2 with f(x) = (D_1(x), D_2(x)). We sayed that this lemma comes from the Borsuk-Ulam-theorem. So we will use it here. By the theorem there exists a point x, s.t. f(x) = f(-x), i.e. D_1(x) = D_1(-x) and D_2(x) = D_2(-x). If D_1(x) = D_1(-x) = 0, then x and -x are in C_1. Similarly for D_2. But if they are both D_1(x) and D_2(x) not 0, then x and -x must belong to C_3.

That's the proof. Q.E.D.

Next time we will discuss the structure of the universe. See you then!

*Source: Hatcher, Allen (2001): Algebraic Topology, URL: http://www.math.cornell.edu/~hatcher/

Source of the pictures: wikipedia.

#algebraic topology #borsuk-ulam #mathexplainsworld

0 notes

hippasos · 9 years

Text

M.E.W.: Bursuk-Ulam

Let's start the topic "math explains world" (M.E.W.) with a result from Algebraic Topology. In its mathematical formulation the theorem looks not very interesting:

If f: S^2 ---> IR^2 is continuous, then there exists a pair of antipodal points x and -x, s.t. f(x) = f(-x), where S^2 denotes the 2-sphere (something which we can imagine as the surface of a ball) and IR^2 is the real number plane.

This theorem is the so-called Borsuk-Ulam-theorem. Stanisław Marcin Ulam, who also was involved in the early development of nuclear weapons, assumed that this theorem might be correct. Karol Borsuk, a Polish mathematician, proved 1933 the theorem.

But why should we be interested in such a boring thing from the last century? Well, I can reassure you, it's not that boring. ;-)

The application of this theorem implies a result which is really mindblowing. Let us consider temperature and pressure on earth. We can imagine the S^2 to be the surface of the earth. Antipodal points on earth are just points which lie on opposite sides of the S^2, like the north and south pole. There is a nice antipodal map on http://www.antipodesmap.com/, which helps to find antipodal points on earth. For example an antipodal point to Berlin would be somewhere in the south-west of New Zealand.

The map f could be a function that assigns points of the earth to a pair of two values, temperature and presssure. If we can assume that this map is continuous, then the theorem says that there is always a pair of antipodal points on earth, which has the same temperature and pressure. Think about this! o.O

But why should this statement true? I will explain it.

!!! WARNING: The following section is written for freaks and nerds who are really interested in the idea of the proof. If you are not of this type, then you should skip the following. ;-) !!!

I will give only the idea of the proof by several pictures. This is not really mathematically correct, but intuitive. Proof: In Algebraic Topology the term of covering spaces is connected with this theme (it's also connected with the term of the fundamental group). What is a covering space? We only have to know what is the covering space of the S^1 (unit circle or 1-sphere) to proof the theorem. The so-called universal covering of the S^1 is a map from p: IR ---> S^1 which has the following properties and is shown in the modified picture from Hatcher's Algebraic Topology book (2001, p. 29).

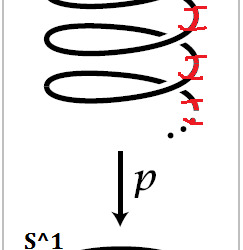
A small (open) neighbourhood U (in red) of an arbitrary point of the S^1 has a bunch of corresponding (open) neighbourhoods in IR (also in red), s.t. we can map them to the first neighbourhood by p and p induces a homeomorphism from one of the neighbourhoods to U, this means that the neighbourhoods are really “similar” to the neighbourhood U. In the following proof we can assume that p(t) = e^(2 pi i t) (cf. https://en.wikipedia.org/wiki/Euler%27s_formula). The proof follows Hatcher’s proof (2001, p. 32,33). Now we are well prepared for the proof. We prove the theorem by assuming the contrary and leading it to a contradiction (https://en.wikipedia.org/wiki/Proof_by_contradiction).

Let's suppose that such a map exists, but has no point x, s.t. f(x) = f(-x). Then we can define the function g: S^2 ---> S^1 with g(x) = (f(x) - f(-x))/|f(x) - f(-x)|. We can calculate just by inserting -x in the formular, that g(-x) = g(x). We call the equator loop (cf. picture down) y: [0,1] ---> S^2, where we choose x_0 as the basepoint of the loop, i.e. 0 and 1 get mapped to x_0 in S^2.

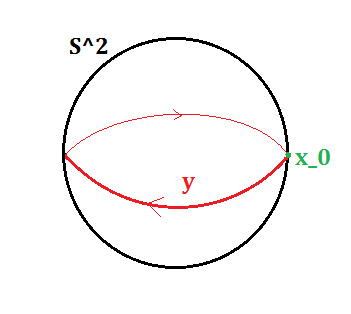
This is indeed a loop, because it starts and ends at the same basepoint x_0. The composition g*y given by g*y(x) = g(y(x)) is a map from [0,1] to S^1 which starts and ends at the same point, hence a loop in S^1.

Since we know that a neighbourhood of a point in S^1 has a bunch of neighbourhoods in IR by the property of the covering space, we can construct a unique path in IR by lifting pieces of the loop g*y in S^1 by this lifting-property of the covering space to IR. This path is unique, if we fix basepoints, i.e. we map 0 in IR to 1 in S^1 by p. (Rmk.: Consider that 1 is in S^1, because we are working in the complex plane. If you are not firm working with complex numbers, just read (1,0) instead of 1 and consider the real number plane IR^2.) We can construct this lifting of the loop in finitely many steps (by compactedness). We call this lifting G*Y which is just a path from [0,1] to IR. So we have G*Y: [0,1] ---> IR. Now we can compare loops in S^1 with paths in IR. An example of the path G*Y in IR (in blue) is given by the following picture:

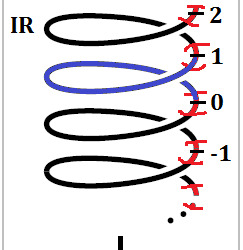
The corresponding loop at the base S^1 is also coloured blue (modified picture from Hatcher, 2001, p. 29).

Let's consider the difference d: [0,1/2] ---> IR given by

d(t) = G*Y(t) - G*Y(t + 1/2) = G(Y(t)) - G(Y(t+ 1/2)).

This difference is just the difference of antipodal points in S^1 in terms of the difference of the corresponding paths in IR. We know, if we go once around the circle S^1, i.e. we have a loop starting and ending at 1 in S^1 (see Rmk. before), then we go from 0 to 1 in IR, like we see it in the picture. If we go 1/2 of the way of the loop g*y in S^1, then we have two antipodal points z and -z in S^1. Now we consider p: IR ---> S^1 given by p(t) = e^{2 pi i t}. Any two antipodal points z and -z in S^1 give integers x in p^{-1}(z) and x' in p^{-1}(-z) which differ just by a number of the form "n + 1/2" where n is an integer. Looking at the preimage p^{-1}(z) or p^{-1}(-z) means just looking at the bunch of points in IR above the points z and -z. But being something of the form "n + 1/2 = (2n + 1)/2 = odd integer/2" means just that the difference

d(t) = G*Y(t) - G*Y(t + 1/2) = q/2, where q is an odd integer.

But then

G*Y(1) - 0 = G*Y(1) - G*Y(0) = G*Y(1) - G*Y(1/2) + G*Y(1/2) - G*Y(0) = (G*Y(1) - G*Y(1/2)) + (G*Y(1/2) - G*Y(0)) = q/2 + q/2 = q.

So G*Y(1) = q not equal to 0 and this means that G*Y starts in 0 and ends in q. But this is a contradiction, because y is homotopic to the constant loop c that stays for its whole interval [0,1] at one point (i.e. c(t) = x_0), i.e. we can deform y in S^2 continuously to a point, like in this picture:

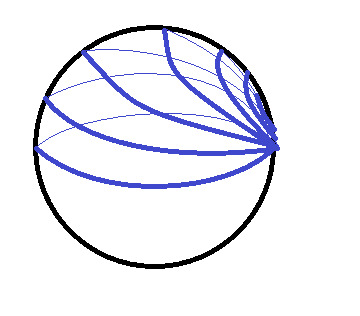
But then g*y is homotopic to a constant loop, hence G*Y, too. But we saw that G*Y doesn't stay at one point, but goes from 0 to q. So it can't be the constant loop. CONTRADICTION!

Q.E.D.

Next time we will look at an interesting consequence of the theorem, which has something to do with a division of the world. But this will not be written before next month. See you then!

Sources:

First picture: https://de.wikipedia.org/wiki/Karol_Borsuk#/media/File:Borsuk.jpeg, https://de.wikipedia.org/wiki/Stanis%C5%82aw_Marcin_Ulam#/media/File:Stanislaw_Ulam_ID_badge.png

Second picture: https://de.wikipedia.org/wiki/Erde#/media/File:The_Earth_seen_from_Apollo_17.jpg

Third and fifth picture: Modified pictures from

Hatcher, Allen (2001): Algebraic Topology, URL: http://www.math.cornell.edu/~hatcher/

#borsuk-ulam #algebraic topology #covering spaces #mathexplainsworld

0 notes

hippasos · 9 years

Text

Math explains universe

"All things are numbers" (Pythagoras)

Pythagoras one of the most popular mathematicians of the ancient Greece, said that "all things are numbers". Although he was referring to the connection between music and arithmetic, people who are not familiar with mathematics often ask me, if mathematics will describe the whole world in some point in future.

I don't think so. But mathematics gives us a powerful tool to describe parts of our universe and our earth. In the following posts I will explain some theorems which mostly come from Algebraic Topology and their interesting application to our world and our universe.

Beside this subject: Pythagoras quote shows one central philosophy of his work as a mathematician. The Pythagoreans believed that all things are explainable as integer proportions. Hippasos of Metapontum, a desciple of Pythagoras, discovered the existence of irrational numbers (i.e. in particular numbers which can’t be described as a quotient of integers). He published his discovery. This induced the first foundational crisis in mathematics! The pythagoreans were very outraged, in particular because Hippasos showed the existence of irrational numbers by using the pythagorean sign, the pentagram, a star with 5 edges. So they threw Hippasos into the sea, where he died.*

Remark: The circumstances of Hippasos death are not really clear!

*Source: Beutelspacher, A.: Albrecht Beutelspachers Kleines Mathematikum: Die 101 wichtigsten Fragen und Antworten zur Mathematik. Verlag C. H. Beck oHG, München 2010, p. 55-57.

Source of the pictures:

1.) https://en.wikipedia.org/wiki/Universe#/media/File:Ilc_9yr_moll4096.png

2.) https://de.wikipedia.org/wiki/Datei:Golden_ratio_-_Pentagram.svg

#hippasos #pythagoras #universe #world #mathematics

0 notes

hippasos · 9 years

Photo

I have to confess that I don’t really know, if childeren in other countries play this game, but in Germany we draw the “house of Saint Nicholas”. And children are saying the syllables

“Das-ist-das-Haus-vom-Ni-ko-laus.”

(Translation: “This-is-the-house-of-Ni-cho-las.”)

for each line they draw, while they draw a house in the way which is shown above. The only rules are the following:

1.) You have to draw the lines without lifting the pen.

2.) You have to draw "complete” straight lines .

There are several ways to do this.

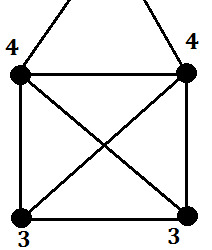
Graph theory sayes something about the existence of drawing such an object. In Graph theory we consider a bunch of vertices which are connected with edges (lines). The Graph for the “Haus vom Nikolaus” is shown in the picture.

The way of drawing the house described above is called an Eulerian trail, i.e. a value of the form

v1 e1 v2 e2 v3 ... e(n-1) v(n)

where e1,...,e(n-1) are the edges and v1,...,vn are the vertices. Such a value has the special property as an Eulerian trail that we go no edge twice or more times.

We also need to know the degree of a vertex. The degree of a vertex is the number of edges which lead to this vertex. For example the degree of the edges of the “Haus vom Nikolaus” is shown in the picture.

One can show the following: If the degree of all edges is even, then there exists an Eulerian cycle, i.e. an Eulerian trail which starts and ends at the same vertex. An Eulerian trail (which is not an Eulerian cycle) exists, if the degree of two edges is odd and the degree of the other edges is even.

If we consider the graph of the “Haus vom Nikolaus”, we see that we have two edges of odd degree (3) and three edges of even degree (2 and 4). So we have an Eulerian trail which is not an Eulerian cycle. This means, that we can draw the “Haus vom Nikolaus” considering the rules described above.

Another interesting object is the problem of the Seven Bridges of Königsberg (1736). You can find a graph decribing the problem. With the rules we formulated above for an Eulerian trail, you can easily check, if it is possible to find a way over the 7 bridges without going a bridge twice or more times. Here is the link of this interesting historic problem which Euler solved:

https://en.wikipedia.org/wiki/Seven_Bridges_of_K%C3%B6nigsberg

#Eulerian trail #Eulerian cycle #graph theory #haus vom nikolaus

1 note · View note

hippasos · 9 years

Photo

Whistler’s mother gifts her son an ungly painting. Whistler doesn’t want to offend his mother. Instead of throwing the painting in the rubbish, he tries to hang up the painting, such that it falls on the floor, if any of the two nails which fix the string of the painting are taken away. But the painting should be hang up securely, i.e. the painting doesn’t fall on the ground for no reason. How should he hang up the painting at two nails? Goup theory gives the answer. We consider the free group Z ✱ Z, generated by S = {a,b}. Consider the loops which are going around the first nail as generated by a and for the second nail generated by b. a and b are the loops which are going around once in clock direction. What means "generated"? This means, that we can write any loop which goes around the first nail n times as something like a^n=a...a (analoge for b), i.e. we are going the loop a n-times. If we want to go backwards we just going a^{-1}, which is against the clock direction. In this case we can write in an analoge way a^{-n} for going n times against the clock direction. It's clear: If we form a loop first going around the nail n times in clock direction and then m times against the clock direction, we have a^{n}a^{-m}. After contracting this loop by the weight of the painting, a^{n}a^{-m} equals a^{n-m}, because loops which are inverse to each other annul each other. For example: If we form a loop which goes 2 times in clock direction and one time against the clock direction, after pulling we have a loop which goes once around the nail in clock direction. This annulation doesn't work, if we consider loops going around the first and second nail alternatingly, for instance: a^{5}b^{-3}a^{2}. Such a combination can be described by using algebraic topology. This concept is linked with free groups and the fundamental group of the figure 8. So how can we form such a loop that the painting falls on the ground, if we just take one nail away? An example is the following where we go ab^{-1}a^{-1}b:

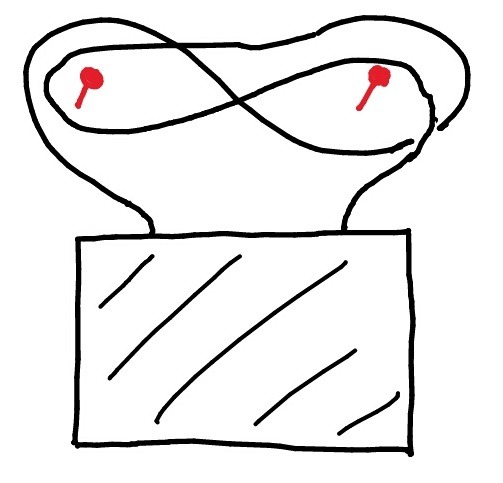
If we take the right nail away we also take the loops a and a^{-1} away and we get b^{-1}b where b and b^{-1} annul each other. The painting falls on the ground. For the same reason the painting falls, if we take the left nail away. With the algebraic considerations we can easily construct an attachment with n nails (n is an integer greater than 2), such that the painting falls on the ground, if we take one nail away.

#algebra #algebraic topology #whistler's mother #painting #group theory

0 notes